Hoạt động1
Trả lời câu hỏi Hoạt động 1 trang 67
Cho tam giác ABC vuông tại A (Hình 1).
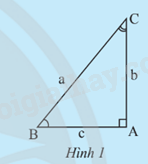
a) Hãy tính sin B theo b và a, cos B theo c và a. Sử dụng các kết quả tính được để giải thích tại sao ta lại có các đẳng thức:
b = a.sin B
c = a.cos B
b) Hãy tính tan B theo b và c, cot B theo c và b. Sử dụng các kết quả tính được ở trên để giải thích tại sao ta lại có các đẳng thức:
b = c.tan B
c = b.cot B.

Dựa vào tỉ số lượng giác của góc nhọn. Xét tam giác vuông ABC:
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin, kí hiệu sin.
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin, kí hiệu cos.
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là tang, kí hiệu tan.
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang , kí hiệu cot.

Xét tam giác vuông ABC, ta có:
a) \(\sin B = \frac{{AC}}{{BC}} = \frac{b}{a}\) suy ra b = a.sin B
\(\cos B = \frac{{AB}}{{BC}} = \frac{c}{a}\) suy ra c = a.cos B
b) \(\tan B = \frac{{AC}}{{AB}} = \frac{b}{c}\) suy ra b = c.tan B
\(\cot B = \frac{{AB}}{{AC}} = \frac{c}{b}\) suy ra c = b.cot B.
Thực hành1
Trả lời câu hỏi Thực hành 1 trang 68
Cho tam giác ABC vuông tại A có độ dài cạnh huyền bằng 20cm. Tính độ dài các cạnh góc vuông trong mỗi trường hợp sau (kết quả làm tròn đến hàng phần trăm)
a) \(\widehat B = {36^o}\)
b) \(\widehat C = {41^o}\)

- Đọc kĩ dữ liệu đề bài để vẽ hình
- Dựa vào định lí: Xét tam giác vuông:
+ Mỗi cạnh góc vuông bằng cạnh huyền nhân sin góc đối hoặc nhân côsin góc kề rồi suy ra cạnh góc vuông và áp dụng định lý Pythagore tính cạnh góc vuông còn lại.
+ Mỗi cạnh góc vuông bằng cạnh góc vuông còn lại nhân tang góc đối hoặc nhân côtang góc kề rồi suy ra cạnh góc vuông và áp dụng định lý Pythagore tính cạnh góc vuông còn lại.
Advertisements (Quảng cáo)

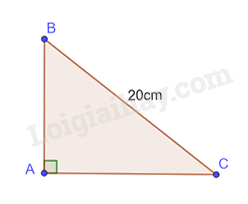
a) Với \(\widehat B = {36^o}\), cạnh góc vuông AB có góc kề bằng \({36^o}\) nên ta có:
AB = cos\({36^o}.BC = 16,18cm\)
Áp dụng định lí Pythagore vào tam giác ABC vuông tại A ta có:
\(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{20}^2} - 16,{{18}^2}} = 11,76cm\)
b) Với \(\widehat C = {41^o}\), cạnh góc vuông AB có góc đối bằng \({41^o}\) nên ta có:
AB = sin\(\widehat C.BC = 13,12cm\)
Áp dụng định lí Pythagore vào tam giác ABC vuông tại A ta có:
\(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{20}^2} - 13,{{12}^2}} = 15,1cm\)
Thực hành2
Trả lời câu hỏi Thực hành 2 trang 68
Tính độ dài cạnh góc vuông x của mỗi tam giác vuông trong Hình 3 (kết quả làm tròn đến hàng phần trăm).
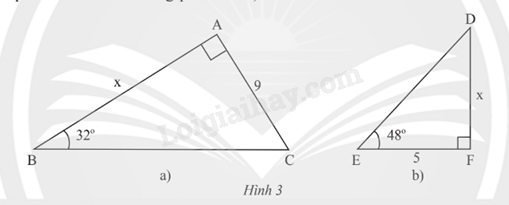

Dựa vào định lí: Xét tam giác vuông:
+ Mỗi cạnh góc vuông bằng cạnh huyền nhân sin góc đối hoặc nhân côsin góc kề rồi suy ra cạnh góc vuông.
+ Mỗi cạnh góc vuông bằng cạnh góc vuông còn lại nhân tang góc đối hoặc nhân côtang góc kề rồi suy ra cạnh góc vuông.

a) Xét tam giác ABC vuông tại A. \(\widehat B = {32^o}\), ta có:
x = AB = AC. cot \({32^o}\) = 9. cot\({32^o}\)\( \approx \) 14,4
b) Xét tam giác DEF vuông tại F. \(\widehat E = {48^o}\), ta có:
x = DF = EF. tan \({48^o}\) = 5. tan \({48^o}\)\( \approx \) 5,55
Vận dụng1
Trả lời câu hỏi Vận dụng 1 trang 68
Một cần cẩu đang nâng một khối gỗ trên sông. Biết tay cần cẩu AB có chiều dài là 16m và nghiêng một góc \({42^o}\) so với phương nằm ngang (Hình 4). Tính chiều dài BC của đoạn dây cáp (kết quả làm tròn đến hàng phần mười).
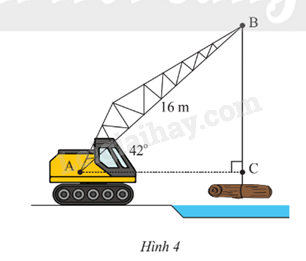

Dựa vào định lí: Xét tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân sin góc đối hoặc nhân côsin góc kề rồi suy ra cạnh góc vuông.

Xét tam giác ABC vuông tại C, \(\widehat A = {42^o}\), ta có:
BC = sin \({42^o}\).AB = sin \({42^o}\).16 = 10,7 m
