
Cho tam giác nhọn ABC có AD, BE, CF là đường cao và H là trực tâm. Chứng minh rằng
a) Tứ giác AEHF, BDHF và CDHE là các tứ giác nội tiếp
b) DA là đường phân giác của góc FDE.

Đọc kĩ dữ kiện để vẽ hình
Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng \({180^o}\).
Áp dụng hai góc nội tiếp cùng chắn một cung thì bằng nhau.

Advertisements (Quảng cáo)
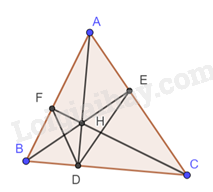
a) Ta có \(\widehat {AEH} = \widehat {AFH} = {90^o}\) (Do CF và BE là đường cao)
suy ra AEHF là tứ giác nội tiếp.
Chứng minh tương tự BDHF và CDHE là các tứ giác nội tiếp
b) Theo phần a ta có BDHF nội tiếp nên \(\widehat {ABE} = \widehat {FDA}\)
DHEC nội tiếp nên \(\widehat {ADE} = \widehat {FCA}\).
Lại có \(\widehat {ABE} = \widehat {FCA}\) (cùng phụ \(\widehat {BAC}\))
Suy ra \(\widehat {FDA} = \widehat {ADE}\) hay AD là đường phân giác của góc FDE.
