Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng \({180^o}\). Hướng dẫn giải bài tập 7.9 trang 38 SGK Toán 9 tập 2 - Cùng khám phá - Bài 2. Tứ giác nội tiếp. Tính số đo các góc của tứ giác nội tiếp CDEF trong Hình 7...
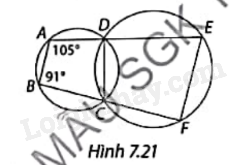
Tính số đo các góc của tứ giác nội tiếp CDEF trong Hình 7.21
Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng \({180^o}\).
Xét tứ giác ABCD nội tiếp đường tròn nên ta có:
Advertisements (Quảng cáo)
\(\widehat {ADC} = {180^o} - \widehat {ABC} = {180^o} - {91^o} = {89^o}\)
Mà \(\widehat {ADE}\) là góc bẹt nên \(\widehat {EDC} = {180^o} - \widehat {ADC} = {180^o} - {89^o} = {91^o}\)
Suy ra \(\widehat {CFE} = {180^o} - \widehat {EDC} = {180^o} - {91^o} = {89^o}\)
\(\widehat {BCD} = {180^o} - \widehat {BAD} = {180^o} - {105^o} = {75^o}\)
Mà \(\widehat {BCF}\) là góc bẹt nên \(\widehat {DCF} = {180^o} - \widehat {BCD} = {180^o} - {75^o} = {105^o}\)
Suy ra \(\widehat {FED} = {180^o} - \widehat {DCF} = {180^o} - {105^o} = {75^o}\).