Góc nội tiếp bằng nửa góc ở tâm cùng chắn một cung Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng \({180^o}\). Giải chi tiết bài tập 7.14 trang 38 SGK Toán 9 tập 2 - Cùng khám phá - Bài 2. Tứ giác nội tiếp. Tính số đo các góc của tứ giác nội tiếp ABCD trong Hình 7.23...

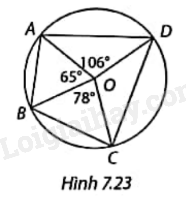
Tính số đo các góc của tứ giác nội tiếp ABCD trong Hình 7.23.

Góc nội tiếp bằng nửa góc ở tâm cùng chắn một cung
Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng \({180^o}\).
Advertisements (Quảng cáo)

Ta có \(\widehat {ADC} = \frac{1}{2}\widehat {AOC} = \frac{1}{2}.\left( {{{65}^o} + {{78}^o}} \right) = 71,{5^o}\) (góc nội tiếp bằng nửa góc ở tâm cùng chắn cung AC)
Suy ra \(\widehat {ABC} = {180^o} - \widehat {ADC} = {180^o} - 71,{5^o} = 108,{5^o}\)
\(\widehat {BCD} = \frac{1}{2}\widehat {BOD} = \frac{1}{2}.\left( {{{65}^o} + {{106}^o}} \right) = 85,{5^o}\)(góc nội tiếp bằng nửa góc ở tâm cùng chắn cung BD)
Suy ra \(\widehat {BAD} = {180^o} - \widehat {BCD} = {180^o} - 85,{5^o} = 94,{5^o}\).
