
Một chiếc đồng hồ trong Hình 7.9 có đường viền là một đường tròn tiếp xúc với ba cạnh của khung đồng hồ hình tam giác đều. Đường kính của đường viền mặt đồng hồ là 10 cm. Khung hình tam giác đều của đồng hồ có độ dài cạnh là bao nhiêu centimet (độ dày đường viền của khung không đáng kể)? Làm tròn kết quả đến hàng phần mười.


Đường tròn nội tiếp của tam giác đều cạnh a có tâm là trọng tâm tam giác đều.
Áp dụng hệ thức lượng trong tam giác vuông để tính cạnh của khung đồng hồ.

Ta có đường kính của đường viền mặt đồng hồ là 10 cm suy ra bán kính r = 5 cm.
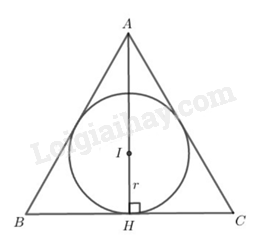
Giả sử tam giác ABC đều có đường tròn nội tiếp tâm I bán kính r
Advertisements (Quảng cáo)
Do đó, I nằm trên đường phân giác góc A.
Gọi H là trung điểm của BC
Mà tam giác ABC đều nên đường phân giác AI cũng là đường trung tuyến, do A, H, I thẳng hàng và AH là đường cao.
I là trọng tâm tam giác ABC nên ta có:
IH = \(\frac{1}{3}\)AH suy AH = 3IH = 3r
Xét tam giác AHB vuông tại H.
\(\widehat B = {60^o}\) (do tam giác ABC đều)
Áp dụng hệ thức lượng trong tam giác vuông ta có:
BH = AH. cot B = AH. cot 60o = 3r .\(\frac{{\sqrt 3 }}{3}\) = r.\(\sqrt 3 \)
Suy ra BC = 2BH = 2r\(\sqrt 3 \) = 2.5.\(\sqrt 3 \) = 10\(\sqrt 3 \approx 17,3cm\).
