Hoạt động3
Đáp án câu hỏi Hoạt động 3 trang 37
Trong Hình 7.17, tứ giác ABCD nội tiếp đường tròn (O). Hãy tính số đo cung nhỏ BD, cung lớn BD, từ đó suy ra số đo góc C. Em có nhận xét gì về tổng hai góc A và C.
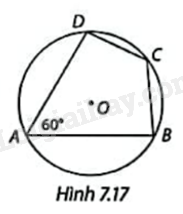

Dùng tính chất góc nội tiếp bằng nửa cung bị chắn để tính cung BD nhỏ và cung BD lớn, sau đó suy ra góc C và kết luận.

Ta có \(\widehat A\) chắn cung nhỏ BD nên \(\widehat{A}=\frac{1}{2}sđ\overset\frown{BD}\) nhỏ suy ra \(sđ\overset\frown{BD}\) nhỏ \( = 2.\widehat A = {2.60^o} = {120^o}\)
Suy ra \(sđ\overset\frown{BD}\) lớn = \({360^o} - {120^o} = {240^o}\)
Mà \(\widehat C\) chắn cung lớn BD nên \(\widehat{C}=\frac{1}{2}sđ\overset\frown{BD}\) lớn = \(\frac{1}{2}{.240^o} = {120^o}\)
Ta có tổng hai góc \(\widehat A + \widehat C = {60^o} + {120^o} = {180^o}\).
Luyện tập3
Hướng dẫn giải câu hỏi Luyện tập 3 trang 38
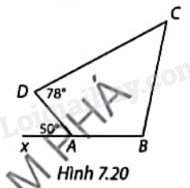
Tính số đo các góc B và C của tứ giác ABCD trong Hình 7.20. Biết tứ giác ABCD nội tiếp được trong đường tròn.

Advertisements (Quảng cáo)
Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng \({180^o}\).

Ta có tứ giác ABCD nội tiếp đường tròn nên \(\widehat D + \widehat B = {180^o}\) suy ra \(\widehat B = {180^o} - \widehat D = {180^o} - {78^o} = {102^o}\)
Ta có \(\widehat {xAB} = {180^o}\)(góc bẹt) suy ra
\(\widehat {DAB} = {180^o} - \widehat {xAD} = {180^o} - {50^o} = {130^o}\)
Mà \(\widehat C + \widehat {DAB} = {180^o}\) suy ra
\(\widehat C = {180^o} - \widehat {DAB} = {180^o} - {130^o} = {50^o}\).
Vận dụng
Giải câu hỏi Vận dụng trang 38
Quay lại phần Khởi động, em hãy sử dụng kiến thức được học về tứ giác nội tiếp để giải thích vì sao không thể tìm được vị trí đặt lửa trại phù hợp.
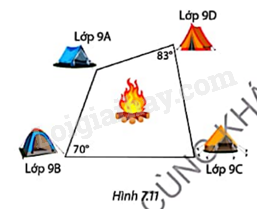
Phần Khởi động: Bốn lớp 9A, 9B, 9C và 9D cùng đi cắm trại. Sử dụng giác kế, các bạn có thể đo được góc tạo bởi các vị trí cắm trại của bốn lớp và vẽ được sơ đồ cắm trại như Hình 7.11. Hỏi có thể tìm được một vị trí cách đều cả bốn trại để đặt lửa trại không?

Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng \({180^o}\).

Không thể tìm được vị trí đặt lửa trại phù hợp vì tổng hai góc đối tạo bởi của lớp 9B và 9B là \({83^o} + {70^o} = {153^o} \ne {180^o}\) nên tứ giác 4 vị trí cắm trại không nội tiếp.
