Hoạt động3
Trả lời câu hỏi Hoạt động 3 trang 60
Hãy chép lại và hoàn thành Bảng 3.2. Em có nhận xét gì về giá trị của \(\sqrt {\left( {x + 1} \right)\left( {x + 3} \right)} \) và \(\sqrt {x + 1} .\sqrt {x + 3} \)?
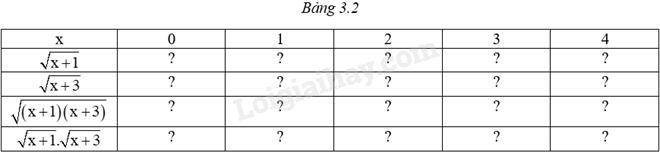

Thay từng giá trị của x vào các căn thức \(\sqrt {\left( {x + 1} \right)\left( {x + 3} \right)} \) và \(\sqrt {x + 1} .\sqrt {x + 3} \) để tính giá trị tương ứng, từ đó rút ra nhận xét.


Ta thấy: \(\sqrt {\left( {x + 1} \right)\left( {x + 3} \right)} = \sqrt {x + 1} .\sqrt {x + 3} \).
Luyện tập3
Trả lời câu hỏi Luyện tập 3 trang 61 SGK Toán 9
Rút gọn các biểu thức sau:
a) \(\sqrt {36{x^8}{{\left( {2 - y} \right)}^2}} \) với \(y \ge 2\);
b) \(\sqrt {\frac{{7z}}{3}} .\sqrt {\frac{3}{{28z}}} \) với \(z > 0\).
Advertisements (Quảng cáo)

Với hai biểu thức A và B không âm, ta có: \(\sqrt {A.B} = \sqrt A .\sqrt B \).

a) \(\sqrt {36{x^8}{{\left( {2 - y} \right)}^2}} \)\( = \sqrt {36} .\sqrt {{x^8}} .\sqrt {{{\left( {2 - y} \right)}^2}} \)\( = 6.\sqrt {{{\left( {{x^4}} \right)}^2}} .\left| {2 - y} \right|\)\( = 6{x^4}\left( {y - 2} \right)\) (vì \(y \ge 2\) nên \(2 - y \le 0\))
b) \(\sqrt {\frac{{7z}}{3}} .\sqrt {\frac{3}{{28z}}} \)\( = \sqrt {\frac{{7z}}{3}.\frac{3}{{28z}}} \)\( = \sqrt {\frac{1}{4}} \)\( = \sqrt {{{\left( {\frac{1}{2}} \right)}^2}} \)\( = \frac{1}{2}\).
Vận dụng1
Trả lời câu hỏi Vận dụng 1 trang 61 SGK Toán 9
Một hình chữ nhật có chiều dài là \(\sqrt {\frac{a}{3}} \) mét và chiều rộng là \(\sqrt {\frac{a}{{12}}} \) (mét) \(\left( {a > 0} \right)\). Tính diện tích của hình chữ nhật theo a.

+ Với hai biểu thức A và B không âm, ta có: \(\sqrt {A.B} = \sqrt A .\sqrt B \).
+ Diện tích hình chữ nhật bằng chiều dài nhân chiều rộng.

Diện tích của hình chữ nhật là:
\(\sqrt {\frac{a}{3}} .\sqrt {\frac{a}{{12}}} = \sqrt {\frac{a}{3}.\frac{a}{{12}}} = \sqrt {\frac{{{a^2}}}{{36}}} = \sqrt {{{\left( {\frac{a}{6}} \right)}^2}} = \left| {\frac{a}{6}} \right| = \frac{a}{6}\) (do \(a > 0\) nên \(\frac{a}{6} > 0\)).
