
Giải tam giác ABC vuông tại A có \(BC = a,AC = b,AB = c,\) trong các trường hợp:
a) \(a = 21,b = 18;\)
b) \(b = 10,\widehat C = {30^0};\)
c) \(c = 5,b = 3.\)

Dựa vào tỉ số lượng giác giữa các cạnh ta tính được góc B hoặc góc C, và các biểu thức liên quan giữa cạnh và góc chưa biết kết hợp thêm định lý Pythagore để tính cạnh còn lại khi biết hai cạnh.

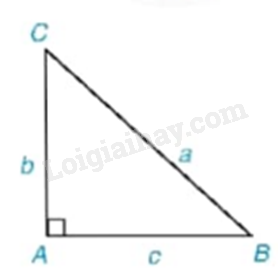
a) \(a = 21,b = 18;\)
Tam giác ABC vuông tại A, ta có: \(A{B^2} + A{C^2} = B{C^2}\) (định lý Pythagore)
Thay số ta có: \(A{B^2} + {18^2} = {21^2}\) hay \(AB = \sqrt {{{21}^2} - {{18}^2}} = 3\sqrt {13} \) (vì \(AB > 0\))
Advertisements (Quảng cáo)
Ta có \(\sin \widehat B = \frac{{AC}}{{BC}} = \frac{{18}}{{21}} = \frac{6}{7}\) nên \(\widehat B \approx {59^0}\)
Mà \(\widehat B + \widehat C = {90^0}\) nên \(\widehat C = {90^0} - \widehat B \approx {90^0} - {59^0} = {31^0}\)
b) \(b = 10,\widehat C = {30^0};\)
Tam giác ABC vuông tại A, ta có \(\tan \widehat C = \frac{{AC}}{{AB}}\) hay \(\tan {30^0} = \frac{{10}}{{AB}}\) suy ra \(AB = \frac{{10}}{{\tan {{30}^0}}} = 10\sqrt 3 \)
\(\sin \widehat C = \frac{{AC}}{{BC}}\) hay \(\sin {30^0} = \frac{{10}}{{BC}}\) suy ra \(BC = \frac{{10}}{{\sin {{30}^0}}} = 20\)
Mà \(\widehat B + \widehat C = {90^0}\) nên \(\widehat C = {90^0} - \widehat B = {90^0} - {30^0} = {60^0}\)
c) \(c = 5,b = 3.\)
Tam giác ABC vuông tại A, ta có: \(A{B^2} + A{C^2} = B{C^2}\) (định lý Pythagore)
Thay số ta có: \(B{C^2} = {5^2} + {3^2} = 34\) hay \(BC = \sqrt {34} \) (vì \(BC > 0\))
Ta có \(\sin \widehat B = \frac{{AC}}{{BC}} = \frac{3}{{\sqrt {34} }}\) nên \(\widehat B \approx {30^0}58’\)
Mà \(\widehat B + \widehat C = {90^0}\) nên \(\widehat C = {90^0} - \widehat B \approx {90^0} - {30^0}57′ = {59^0}02’\)
