Luyện tập3
Trả lời câu hỏi Luyện tập 3 trang 77
Cho tam giác vuông ABC có cạnh góc vuông AB = 4, cạnh huyền BC = 8. Tính cạnh AC (làm tròn đến số thập phân thứ ba) và các góc B, C (làm tròn đến độ).

Từ định lý Pythagore ta tính được cạnh còn lại của tam giác ABC, và dựa vào tỉ số lượng giác của góc B và góc C, ta tính được góc B và góc C.

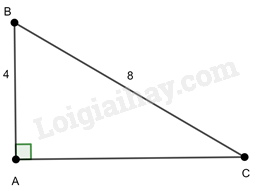
Tam giác ABC vuông tại A nên ta có: \(B{C^2} = {\rm{A}}{{\rm{B}}^2} + A{C^2}\) (Định lý Pythagore)
Thay số ta có: \({8^2} = {4^2} + A{C^2}\) hay \(A{C^2} = {8^2} - {4^2} = 48\) suy ra \(AC = \sqrt {48} = 4\sqrt 3 \)
Ta có: \(\cos \widehat B = \frac{{AB}}{{BC}} = \frac{4}{8} = \frac{1}{2}\) suy ra \(\widehat B = {60^0}\)
\(\sin \widehat C = \frac{{AB}}{{BC}} = \frac{4}{8} = \frac{1}{2}\) suy ra \(\widehat C = {30^0}\)
Câu hỏi
Trả lời câu hỏi Câu hỏi trang 77
1. Hãy nêu cách giải tam giác ABC vuông tại A khi biết hai cạnh \(AB = c,AC = b\) hoặc \(AB = c,BC = a\) và không sử dụng định lý Pythagore (H.4.21).
2. Hãy nêu cách giải tam giác ABC vuông tại A khi biết cạnh góc vuông AB (hoặc cạnh huyền BC) và góc B.
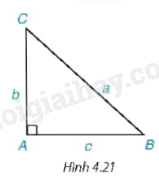

Để giải tam giác vuông ngoài sử dụng định lý Pythagore ta có thể sử dụng tỉ số lượng giác.

1. Trường hợp biết \(AB = c,AC = b\)
Tam giác ABC vuông tại A nên ta có: \(\tan \widehat B = \frac{b}{c}\) từ đó ta tính được góc B, và tính được góc C thông qua định lý tổng ba góc trong một tam giác. Sau khi tính được góc B, ta dùng tỉ số lượng giác \(\cos \widehat B = \frac{c}{{CB}}\) từ đó ta tính được \(CB = \frac{c}{{\cos \widehat B}}\)
Trường hợp \(AB = c,BC = a\)
Tam giác ABC vuông tại A nên ta có: \(\cos \widehat B = \frac{b}{c}\) từ đó ta tính được góc B, và tính được góc C thông qua định lý tổng ba góc trong một tam giác. Sau khi tính được góc B, ta dùng tỉ số lượng giác \(\tan \widehat B = \frac{{AC}}{c}\) từ đó ta tính được \(AC = c.\tan \widehat B\)
2. Tam giác ABC vuông tại A khi biết cạnh góc vuông AB (hoặc cạnh huyền BC) và góc B.
Trường hợp biết cạnh góc vuông AB và góc B
Biết góc B ta tính được góc C thông qua định lý tổng ba góc trong một tam giác. Để tính cạnh BC ta dùng tỉ số lượng giác \(\cos \widehat B = \frac{c}{{BC}}\) từ đó ta tính được \(BC = \frac{c}{{\cos \widehat B}}\) và tỉ số lượng giác \(\tan \widehat B = \frac{{AC}}{c}\) từ đó ta tính được \(AC = c.\tan \widehat B\)
Advertisements (Quảng cáo)
Trường hợp biết cạnh huyền BC và góc B
Biết góc B ta tính được góc C thông qua định lý tổng ba góc trong một tam giác. Để tính cạnh AB ta dùng tỉ số lượng giác \(\cos \widehat B = \frac{{AB}}{a}\) từ đó ta tính được \(AB = a.\cos \widehat B\) và tỉ số lượng giác \(\sin \widehat B = \frac{{AC}}{a}\) từ đó ta tính được \(AC = a.\sin \widehat B\)
Luyện tập4
Trả lời câu hỏi Luyện tập 4 trang 77
Giải tam giác ABC vuông tại A, biết \(BC = 9,\widehat C = {53^0}.\)

Giải tam giác vuông là tìm tất cả các cạnh và các góc chưa biết của tam giác vuông đó thông qua các tỉ số lượng giác hoặc định lý Pythagore.

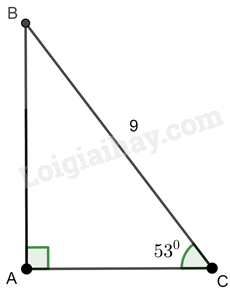
Tam giác ABC vuông tại A nên ta có: \(\cos \widehat C = \frac{{AC}}{{BC}}\) hay \(\cos {53^0} = \frac{{AC}}{9}\) suy ra \(AC = 9.\cos {53^0} \approx 5,42\)
\(\sin \widehat C = \frac{{AB}}{{BC}}\) hay \(\sin {53^0} = \frac{{AB}}{9}\) suy ra \(AB = 9.\sin {53^0} \approx 7,19\)
Ta có: \(\widehat A + \widehat B + \widehat C = {180^0}\) nên \({90^0} + \widehat B + {53^0} = {180^0}\) suy ra \(\widehat B = {37^0}.\)
Vận dụng
Trả lời câu hỏi Vận dụng trang 77
Giải bài toán ở tình huống mở đầu với \(\alpha = {27^0},\beta = {19^0}.\)
Tình huống mở đầu: Để đo chiều cao của một tòa lâu đài (H.4.11) , người ta đặt giác kế thẳng đứng tại M. Quay ống ngắm của giác kế sao cho nhìn thấy đỉnh P’ của tòa lâu đài dưới góc nhọn \(\alpha \). Sau đó, đặt giác kế thẳng đứng tại N, NM = 20 m, thì nhìn thấy đỉnh P’ dưới góc nhọn \(\beta \left( {\beta < \alpha } \right).\) Biết chiều cao giác kế là 1,6 m, hãy tính chiều cao của tòa lâu đài.
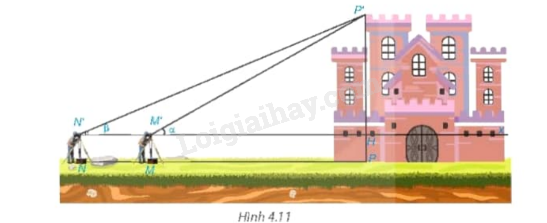

Ta thấy trong hình có hai tam giác vuông P’N’H và P’HM’ có cùng chiều cao từ đó ta tính được chiều cao của tam giác thông qua tỉ số lượng giác của góc \(\alpha ,\beta \) trong hai tam giác vuông và lập được phương trình. Chú ý để tính chiều cao của tòa lâu đài cần tính tổng chiều cao của giác kế và P’H. Độ dài đoạn MN bằng M’N’.

Ta có: \(\tan \alpha = \frac{{P’H}}{{M’H}}\) hay \(P’H = M’H.\tan {27^0}\)
\(\tan \beta = \frac{{P’H}}{{N’H}}\) hay \(P’H = N’H.\tan {19^0}\)
Từ đó ta có phương trình: \(M’H.\tan {27^0} = N’H.\tan {19^0}\) hay \(M’H.\tan {27^0} = \left( {M’H + 20} \right).\tan {19^0}\) suy ra \(M’H.\left( {\tan {{27}^0} - \tan {{19}^0}} \right) = 20.\tan {19^0}\) nên \(M’H = \frac{{20.\tan {{19}^0}}}{{\left( {\tan {{27}^0} - \tan {{19}^0}} \right)}} \approx 41,69\) m
\(P’H = M’H.\tan {19^0} \approx 14,35\) m
Chiều cao của tòa lâu đài khoảng: \(14,35 + 1,6 = 15,95\) m.
