
Cho đường tròn (O; 5 cm).
a) Hãy nêu cách vẽ dây AB sao cho khoảng cách từ điểm O đến dây AB bằng 2,5 cm.
b) Tính độ dài của dây AB trong câu a (làm tròn đến hàng phần trăm).
c) Tính số đo và độ dài của cung nhỏ AB.
d) Tính diện tích hình quạt tròn ứng với cung nhỏ AB.

a) Vẽ bán kính OM của đường tròn, trên OM lấy điểm H sao cho OH = 2,5 cm. Kẻ đoạn thẳng AB vuông góc với OH tại H.
b) Ta chứng minh \(AH = BH\)\( \Rightarrow AB = 2AH\). Áp dụng định lý Pythagore để tính AH, từ đó suy ra độ dài AB.
c) Tính \(\sin \widehat {AOH}\) suy ra \(\widehat {AOH}\)và sđ\(\overset\frown{AB}\), từ đó tính được độ dài cung \(\overset\frown{AB}\).
d) Áp dụng công thức tính diện tích hình quạt tròn.

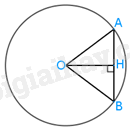
a) Vẽ bán kính OM của đường tròn, trên OM lấy điểm H sao cho OH = 2,5 cm. Kẻ đoạn thẳng AB vuông góc với OH tại H, cắt đường tròn tại A và B ta được dây cung AB cần vẽ.
b) Gọi H là trung điểm của AB.
Advertisements (Quảng cáo)
Xét tam giác OAH và tam giác OBH có:
OA = OB = R
Cạnh OH chung
\(\widehat {OHA} = \widehat {OHB} = 90^\circ \)
\( \Rightarrow \Delta OAH = \Delta OBH\)(cạnh huyền – cạnh góc vuông)
\( \Rightarrow AH = BH\)(hai cạnh tương ứng) \( \Rightarrow AB = 2AH\)
Xét tam giác OAH vuông tại H có: \(A{H^2} + O{H^2} = O{A^2}\)(định lý Pythagore)
hay \(A{H^2} = O{A^2} - O{H^2} = {5^2} - 2,{5^2} = 18,75 \Rightarrow AH = 2,5\sqrt 3 \)(cm)
\( \Rightarrow AB = 2.2,5\sqrt 3 = 5\sqrt 3 \)(cm)
c) Xét tam giác OAH vuông tại H có: \(\sin \widehat {AOH} = \frac{{AH}}{{OA}} = \frac{{2,5\sqrt 3 }}{5} = \frac{{\sqrt 3 }}{2} \Rightarrow \widehat {AOH} = 60^\circ \)
Mà: \(\Delta OAH = \Delta OBH\)\( \Rightarrow \widehat {BOH} = \widehat {AOH} = 60^\circ \)(hai góc tương ứng)
\( \Rightarrow \widehat {AOB} = \widehat {BOH} + \widehat {AOH} = 60^\circ + 60^\circ = 120^\circ \)
\( \Rightarrow \) sđ\(\overset\frown{AB}=120{}^\circ \)
Độ dài cung AB là: \(\frac{{120}}{{180}}.\pi .5 = \frac{{10}}{3}\pi \)(cm)
d) Diện tích hình quạt tròn ứng với cung nhỏ AB là: \(\frac{{{\rm{120}}}}{{{\rm{360}}}}{\rm{.\pi }}{\rm{.5 = }}\frac{{\rm{\pi }}}{{{\rm{10}}}}\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\)
