Chứng minh đường thẳng đi qua A là và song song với BC là tiếp tuyến tức là đường thẳng đó vuông góc với bán kính (hoặc đường kính) tại. Lời Giải bài tập 5.21 trang 103 SGK Toán 9 tập 1 - Kết nối tri thức Bài 16. Vị trí tương đối của đường thẳng và đường tròn. Cho đường tròn (O) đi qua ba đỉnh A, B và C của một tam giác cân tại A, Chứng minh rằng đường thẳng đi qua A và song song với BC là một tiếp tuyến của (O)...

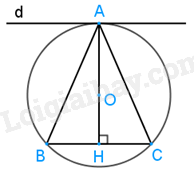
Cho đường tròn (O) đi qua ba đỉnh A, B và C của một tam giác cân tại A, Chứng minh rằng đường thẳng đi qua A và song song với BC là một tiếp tuyến của (O).

Chứng minh đường thẳng đi qua A là và song song với BC là tiếp tuyến tức là đường thẳng đó vuông góc với bán kính (hoặc đường kính) tại điểm A.

Advertisements (Quảng cáo)
Ta có đường thẳng AO là trục đối xứng của đường tròn.
Nên B là điểm đối xứng của C qua AO.
Gọi H là giao điểm của AO và BC.
Khi đó ta có: AH \( \bot \) BC mà d // BC nên AH \( \bot \) d.
Vậy d là một tiếp tuyến của đường tròn.
