Bài 5.6 trang 90 Toán 9 Kết nối tri thức tập 1: Cho đường tròn (O; 5 cm) và AB là một dây bất kì của đường tròn đó...

Cho đường tròn (O; 5 cm) và AB là một dây bất kì của đường tròn đó. Biết AB = 6 cm.

a) Tính khoảng cách từ O đến đường thẳng AB.

b) Tính$\tan \alpha$nếu góc ở tâm chắn cung AB bằng $2\alpha .$

a) Gọi H là trung điểm của AB, chứng minh $OH \bot AB$ hay khoảng cách từ O đến đường thẳng AB bằng độ dài đoạn OH. Sau đó áp dụng định lý Pythagore để tính OH.

b) $\widehat {AOB} = 2\alpha \Rightarrow \alpha = \widehat {HOA}$. Xét tam giác OAH để tính $\tan \alpha .$

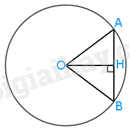
a) Gọi H là trung điểm của AB.

Suy ra: $AH = \frac{{AB}}{2} = \frac{6}{2} = 3$

Xét tam giác OAH và tam giác OBH có:

OA = OB = R

Cạnh OH chung

HA = HB (do H là trung điểm của AB)

Suy ra: $\Delta OAH = \Delta OBH$(c.c.c)

$\Rightarrow \widehat {OHA} = \widehat {OHB}$ (hai góc tương ứng)

Mà $\widehat {OHB}$ và $\widehat {OHB}$ là hai góc bù nhau nên $\widehat {OHA} + \widehat {OHB} = 180^\circ$

$\Rightarrow 2\widehat {OHB} = 180^\circ \Rightarrow \widehat {OHA} = \widehat {OHB} = 90^\circ$ hay $OH \bot AB$

Do đó khoảng cách từ O đến đường thẳng AB bằng độ dài đoạn OH.

Xét tam giác OAH vuông tại H có: $A{H^2} + O{H^2} = O{A^2}$(định lý Pythagore)

hay $O{H^2} = O{A^2} - A{H^2} = {5^2} - {3^2} = 16 \Rightarrow OH = 4$ (cm)

Vậy khoảng cách từ O đến đường thẳng AB bằng 4 cm.

b) Theo giả thiết, góc ở tâm chắn cung AB là $\widehat {AOB} = 2\alpha$

Mà theo câu a) $\Delta OAH = \Delta OBH \Rightarrow \widehat {HOA} = \widehat {HOB}$ (2 góc tương ứng)

Lại có: $\widehat {HOA} + \widehat {HOB} = \widehat {AOB} \Rightarrow 2\widehat {HOA} = 2\alpha \Rightarrow \widehat {HOA} = \alpha$

Suy ra: $\tan \alpha = \frac{{AH}}{{OH}} = \frac{3}{4}$