
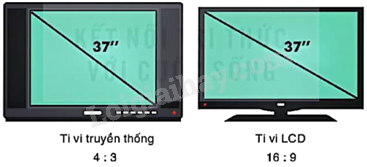
Kích thước màn hình ti vi hình chữ nhật được xác định bằng độ dài đường chéo. Ti vi truyền thống có định dạng 4:3, nghĩa là tỉ lệ giữa chiều dài và chiều rộng của màn hình là 4:3. Hỏi diện tích của màn hình ti vi truyền thống 37in là bao nhiêu? Diện tích của màn hình ti vi LCD 37 in có định dạng 16:9 là bao nhiêu? Màn hình ti vi nào có diện tích lớn hơn? Ở đây, các diện tích màn hình được tính bằng inch vuông.

+ Gọi chiều dài của ti vi là x, đặt điều kiện, tính chiều rộng theo x.
+ Áp dụng định lý Pythagore để đưa ra phương trình theo ẩn x.
+ Giải phương trình ẩn x, tìm nghiệm x, đối chiếu với điều kiện để tìm giá trị x thỏa mãn điều kiện.
+ Tính diện tích của ti vi.
+ So sánh diện tích của ti vi truyền thống và ti vi LCD và đưa ra kết luận.

+) Gọi chiều dài của ti vi truyền thống là x (in, \(x > 0\)) thì chiều rộng của ti vi truyền thống là \(\frac{3}{4}x\left( {in} \right)\)
Advertisements (Quảng cáo)
Khi đó ta có: \({x^2} + {\left( {\frac{3}{4}x} \right)^2} = {37^2}\) (định lý Pythagore)
\(\frac{{25}}{{16}}{x^2} = 1369\)
\(x = \frac{{148}}{5}\) (do \(x > 0\))
Diện tích của ti vi truyền thống là: \(\frac{{148}}{5}.\frac{3}{4}.\frac{{148}}{5} = 675,12\left( {i{n^2}} \right)\)
+) Gọi chiều dài của ti vi LCD là y (in, \(y > 0\)) thì chiều rộng của ti vi LCD là \(\frac{9}{{16}}y\left( {in} \right)\)
Khi đó ta có: \({y^2} + {\left( {\frac{9}{{16}}y} \right)^2} = {37^2}\) (định lý Pythagore)
\(\frac{{337}}{{256}}{y^2} = 1369\)
\({y^2} = \frac{{350464}}{{337}}\)
Diện tích của ti vi LCD là:
\(\frac{9}{{16}}{y^2} = \frac{9}{{16}}.\frac{{350464}}{{337}} = \frac{{197136}}{{337}}\left( {i{n^2}} \right)\)
Vì \(\frac{{197136}}{{337}} < 675,12\) nên màn hình ti vi truyền thống có diện tích lớn hơn.
