Đường tròn nội tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{6}a\). Hướng dẫn giải Giải bài tập 9.11 trang 76 SGK Toán 9 tập 2 - Kết nối tri thức - Bài 28. Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác . Cho tam giác đều ABC ngoại tiếp đường tròn (I).
Câu hỏi/bài tập:

Cho tam giác đều ABC ngoại tiếp đường tròn (I). Tính độ dài các cạnh của tam giác ABC biết rằng bán kính của (I) bằng 1cm.

Đường tròn nội tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{6}a\).
Advertisements (Quảng cáo)

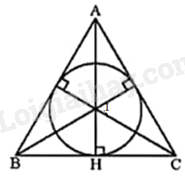
Vì tam giác ABC ngoại tiếp đường tròn (I) và bán kính đường tròn (I) nội tiếp tam giác đều ABC bằng 1cm nên ta có: \(1 = \frac{{\sqrt 3 }}{6}BC \Rightarrow BC = 2\sqrt 3 \left( {cm} \right)\).
Vậy độ dài cạnh tam giác đều bằng \(2\sqrt 3 cm\).
