Câu hỏi/bài tập:

Cho đường tròn (I) nội tiếp tam giác ABC với các tiếp điểm trên các cạnh AB, AC lần lượt là E, F. Chứng minh rằng \(\widehat {EIF} + \widehat {BAC} = {180^o}\)

+ Chứng minh \(\widehat {IFA} = \widehat {AEI} = {90^o}\)
+ Sử dụng tổng các góc trong tứ giác AEIF tính được tổng \(\widehat {EIF} + \widehat {BAC} = {180^o}\).
Advertisements (Quảng cáo)

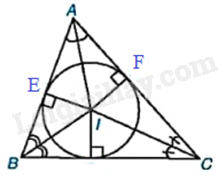
Vì đường tròn (I) nội tiếp tam giác ABC với các tiếp điểm trên các cạnh AB, AC lần lượt là E, F nên \(IF \bot AC,IE \bot AB \Rightarrow \widehat {IFA} = \widehat {AEI} = {90^o}\).
Tứ giác AEIF có: \(\widehat {EAF} + \widehat {EIF} + \widehat {IFA} + \widehat {AEI} = {360^o}\) \( \Rightarrow \widehat {EIF} + \widehat {EAF} = {360^o} - \left( {\widehat {IFA} + \widehat {AEI}} \right) = {180^o}\)
Vậy \(\widehat {EIF} + \widehat {BAC} = {180^o}\).
