Câu hỏi/bài tập:
Cho tứ giác ABCD có \(\widehat A = \widehat C = {90^o}\) (H.9.28). Hãy giải thích vì sao bốn đỉnh của tứ giác ABCD cùng nằm trên một đường tròn có tâm là trung điểm O của đoạn thẳng BD.
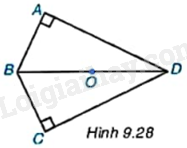

+ Do tam giác ABD vuông tại A nên ba điểm A, B, D thuộc đường tròn đường kính BD với trung điểm của BD là tâm.
Advertisements (Quảng cáo)
+ Vì tam giác CBD vuông tại C nên ba điểm C, B, D thuộc đường tròn đường kính BD với trung điểm của BD là tâm.

Vì tam giác ABD vuông tại A nên ba điểm A, B, D thuộc đường tròn đường kính BD. Mà O là trung điểm của BD nên ba điểm A, B, D thuộc đường tròn (O).
Vì tam giác CBD vuông tại C nên ba điểm C, B, D thuộc đường tròn đường kính BD. Mà O là trung điểm của BD nên ba điểm C, B, D thuộc đường tròn (O).
Do đó, 4 đỉnh của tứ giác ABCD cùng nằm trên một đường tròn có tâm là trung điểm O của BD.
