Câu hỏi/bài tập:
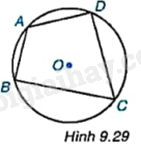
Trên đường tròn (O), lấy các điểm A, B, C, D sao cho tứ giác ABCD là tứ giác lồi (H.9.29). Các đường trung trực của các cạnh AB, BC, CD, DA có đồng quy hay không?

+ Gọi E là trung điểm của AD.
+ Chứng minh được OE là đường trung trực của AD.
+ Chứng minh tương tự ta có các đường trung trực của các cạnh AB, BC, CD cũng đi qua O.
+ Vậy các đường trung trực của các cạnh AB, BC, CD, DA có đồng quy.
Advertisements (Quảng cáo)

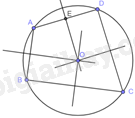
Gọi E là trung điểm của AD. Tam giác AOD cân tại O (do \(OA = OD\)) nên OE là đường trung tuyến đồng thời là đường cao trong tam giác. Do đó, \(OE \bot AD\) tại E.
Vì \(OE \bot AD\) tại E và E là trung điểm của AD nên OE là đường trung trực của AD.
Do đó, đường trung trực của đoạn thẳng AD đi qua O.
Chứng minh tương tự ta có: Các đường trung trực của các cạnh AB, BC, CD đi qua O.
Vậy các đường trung trực của các cạnh AB, BC, CD, DA có đồng quy.
