Câu hỏi/bài tập:
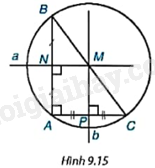
Cho tam giác ABC vuông tại đỉnh A (H.9.15). Gọi N, P lần lượt là trung điểm của các cạnh AB và AC.
a) Vẽ hai đường trung trực a, b của các cạnh AB, AC, cắt nhau tại M.
b) Hãy giải thích vì sao MN, MP là các đường trung bình của tam giác ABC.
c) Hãy giải thích vì sao M là trung điểm của BC, từ đó suy ra đường tròn ngoại tiếp của tam giác ABC có tâm M và bán kính \(MB = MC = \frac{{BC}}{2}\).

a) Vẽ đường thẳng a vuông góc với AB tại N thì a là đường trung trực của cạnh AB.
Vẽ đường thẳng b vuông góc với AC tại P thì b là đường trung trực của cạnh AC.
b) + Chứng minh a//AC, b//AB.
+ Sử dụng tính chất: Trong một tam giác, nếu một đường thẳng đi qua trung điểm một cạnh và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba chứng minh được MN, MP là các đường trung bình của tam giác ABC.
c) Chứng minh tứ giác ANMP là hình chữ nhật, suy ra \(\widehat {NMP} = {90^o}\).
Chứng minh được \(\widehat {BMN} = {180^o}\) nên 3 điểm M, B, C thẳng hàng. Mà \(MB = MC = AM\), M là trung điểm của BC. Từ đó suy ra đường tròn ngoại tiếp của tam giác ABC có tâm M và bán kính \(MB = MC = \frac{{BC}}{2}\).

Advertisements (Quảng cáo)
a) Vẽ đường thẳng a vuông góc với AB tại N thì a là đường trung trực của cạnh AB.
Vẽ đường thẳng b vuông góc với AC tại P thì b là đường trung trực của cạnh AC.
b) Vì tam giác ABC vuông tại A nên \(AB \bot AC\), vì a là trung trực của AB nên \(a \bot AB\), suy ra: a//AC.
Vì b là đường trung trực của AC nên \(b \bot AC\), mà \(AB \bot AC\)(cmt) nên b//AB.
Xét tam giác ABC có:
+ Vì a//AC, mà N là trung điểm của AB nên đường thẳng a đi qua trung điểm của BC. Do đó, MN là đường trung bình của tam giác ABC.
+ Vì b//AB, mà P là trung điểm của AC nên đường thẳng b đi qua trung điểm của BC. Do đó, MP là đường trung bình của tam giác ABC.
c) Tứ giác ANMP có: \(\widehat {NAP} = \widehat {MPA} = \widehat {MNA} = {90^o}\) nên tứ ANMP là hình chữ nhật. Do đó, \(\widehat {NMP} = {90^o}\).
Vì M thuộc đường trung trực của AB nên \(BM = MA\). Suy ra, tam giác BAM cân tại M. Do đó, MN là đường trung trực đồng thời là đường phân giác của tam giác. Do đó, \(\widehat {BMN} = \widehat {NMA}\).
Vì M thuộc đường trung trực của AC nên \(MA = MC\). Suy ra, tam giác CAM cân tại M. Do đó, MP là đường trung trực đồng thời là đường phân giác của tam giác. Do đó, \(\widehat {CMP} = \widehat {PMA}\).
Ta có: \(\widehat {BMC} = \widehat {BMN} + \widehat {NMA} + \widehat {AMP} + \widehat {PMC} = 2\left( {\widehat {NMA} + \widehat {AMP}} \right) = 2.\widehat {NMP} = {180^o}\)
Do đó, ba điểm M, B, C thẳng hàng. Suy ra, \(MA = MB = MC = \frac{{BC}}{2}\).
Suy ra, đường tròn ngoại tiếp của tam giác ABC có tâm M và bán kính \(MB = MC = \frac{{BC}}{2}\).
