Câu hỏi/bài tập:
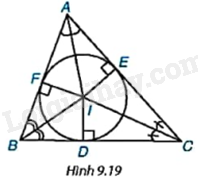
Cho tam giác ABC có ba đường phân giác đồng quy tại điểm I. Gọi D, E, F lần lượt là chân các đường vuông góc kẻ từ I xuống các cạnh BC, CA và AB (H.9.19).
a) Hãy giải thích vì sao các điểm D, E, F cùng nằm trên một đường tròn có tâm I.
b) Gọi (I) là đường tròn trên. Hãy giải thích vì sao (I) tiếp xúc với các cạnh của tam giác ABC.
a) Sử dụng tính chất: Giao điểm của ba đường phân giác trong tam giác cách đều ba cạnh của tam giác, do đó \(IE = ID = FI\).
b) Vì \(IE \bot AC\left( {E \in AC} \right),IE = R\) nên AC tiếp xúc với đường tròn (I; R) tại E, tương tự ta chứng minh được đường tròn (I) tiếp xúc với các cạnh của tam giác ABC.
a) Vì D, E, F lần lượt là chân các đường vuông góc kẻ từ I xuống các cạnh BC, CA và AB nên \(IF \bot AB,IE \bot AC,ID \bot BC\).
Vì I là giao điểm của ba đường phân giác nên I cách đều ba cạnh AB, AC, CB. Do đó, \(IE = IF = ID\)
Do đó, ba điểm D, E, F cùng nằm trên một đường tròn có tâm I.
b) Gọi \(IE = IF = ID = R\) nên ba điểm D, E, F cùng nằm trên đường tròn (I; R).
Vì \(IE \bot AC\left( {E \in AC} \right),IE = R\) nên AC tiếp xúc với đường tròn (I; R) tại E.
Vì \(IF \bot AB\left( {F \in AB} \right),IF = R\) nên AB tiếp xúc với đường tròn (I; R) tại F.
Vì \(ID \bot BC\left( {D \in BC} \right),ID = R\) nên BC tiếp xúc với đường tròn (I; R) tại D.
Vậy đường tròn (I) ở trên tiếp xúc với các cạnh của tam giác ABC.