Vì tam giác ABC đều nội tiếp đường tròn (O) nên O là trọng tâm. Hướng dẫn giải Câu hỏi Luyện tập 2 trang 74 SGK Toán 9 Kết nối tri thức - Bài 28. Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác.
Câu hỏi/bài tập:
Cho tam giác đều ABC nội tiếp đường tròn (O) có bán kính bằng 4cm. Tính độ dài các cạnh của tam giác ABC.
+ Vì tam giác ABC đều nội tiếp đường tròn (O) nên O là trọng tâm, trực tâm của tam giác ABC.
+ Gọi H là giao điểm của AO và BC nên AH là trung trực đồng thời là đường cao trong tam giác đều ABC. Do đó: \(OA = \frac{{BC\sqrt 3 }}{3}\), từ đó tính được BC.
Advertisements (Quảng cáo)
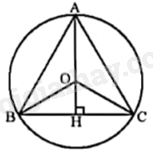
Vì tam giác ABC đều nội tiếp đường tròn (O) nên O là trọng tâm, trực tâm của tam giác ABC.
Gọi H là giao điểm của AO và BC nên AH là trung trực đồng thời là đường cao trong tam giác đều ABC.
Do đó: \(OA = \frac{{BC\sqrt 3 }}{3} \Rightarrow BC = \sqrt 3 OA = 4\sqrt 3 \left( {cm} \right)\).
Vậy cạnh của tam giác đều bằng \(4\sqrt 3 cm\).