Câu hỏi/bài tập:
Cho tam giác ABC đều có trọng tâm G.
a) Giải thích vì sao G cũng là tâm đường tròn nội tiếp tam giác ABC.
b) Từ đó, giải thích vì sao bán kính đường tròn nội tiếp tam giác ABC bằng một nửa đường tròn ngoại tiếp tam giác ABC và bằng \(\frac{{\sqrt 3 }}{6}BC\).

a) Sử dụng tính chất: Trong tam giác đều, trọng tâm đồng thời là giao điểm của ba đường phân giác. Suy ra, G là tâm đường tròn nội tiếp tam giác ABC.
b) + Gọi D là giao điểm của AG và CB. Khi đó, GD là bán kính đường tròn đường tròn nội tiếp tam giác ABC, AG là bán kính đường tròn ngoại tiếp tam giác ABC.
+ Theo tính chất của trọng tâm trong tam giác ABC ta có: \(GD = \frac{1}{2}AG = \frac{1}{3}AD\).
+ Theo định lý Pythagore vào tam giác ADC vuông tại D tính được: \(AD = \frac{{BC\sqrt 3 }}{2}\), nên \(GD = \frac{{\sqrt 3 }}{6}BC\).

Advertisements (Quảng cáo)
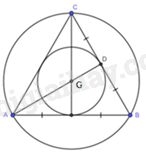
a) Tam giác ABC đều nên G là trọng tâm của tam giác ABC đồng thời là giao điểm của ba đường phân giác. Do đó, G là tâm đường tròn nội tiếp tam giác ABC.
b) Vì G là giao điểm của ba đường trung trực trong tam giác đều ABC (do G là trọng tâm tam giác ABC) nên G là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi D là giao điểm của AG và CB. Suy ra, AG là bán kính đường tròn ngoại tiếp tam giác ABC.
Tam giác ABC đều nên AD là đường trung tuyến đồng thời là đường cao trong tam giác. Do đó, \(GD \bot CB\) tại D. Suy ra, GD là bán kính đường tròn nội tiếp tam giác ABC.
Vì G là trọng tâm tam giác ABC nên \(GD = \frac{1}{2}AG = \frac{1}{3}AD\).
Áp dụng định lý Pythagore vào tam giác ADC vuông tại D có:
\(A{D^2} + C{D^2} = A{C^2} \Rightarrow AD = \sqrt {A{C^2} - C{D^2}} = \sqrt {B{C^2} - \frac{{B{C^2}}}{4}} = \frac{{BC\sqrt 3 }}{2}\)
Do đó, \(GD = \frac{1}{3}.\frac{{BC\sqrt 3 }}{2} = \frac{{\sqrt 3 }}{6}BC\).
Vậy bán kính đường tròn nội tiếp tam giác ABC bằng một nửa đường tròn ngoại tiếp tam giác ABC và bằng \(\frac{{\sqrt 3 }}{6}BC\).
