Câu hỏi/bài tập:
Cho tam giác đều ABC (H.9.22).
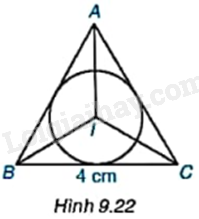
a) Vẽ đường tròn (I; r) nội tiếp tam giác ABC.
b) Biết rằng \(BC = 4cm\), hãy tính bán kính r.
a) + Vẽ ba đường phân giác của tam giác ABC.
+ Gọi I là giao điểm của ba đường phân giác đó.
+ Gọi H là giao điểm của AI và BC. Vẽ đường tròn tâm I, bán kính IH.
+ Khi đó, đường tròn (I; IH) là đường tròn nội tiếp tam giác ABC cần vẽ.
b) Đường tròn nội tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{6}a\)
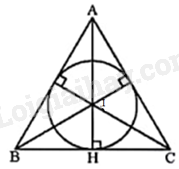
a) Vẽ ba đường phân giác của tam giác ABC. Gọi I là giao điểm của ba đường phân giác đó.
Gọi H là giao điểm của AI và BC. Vẽ đường tròn tâm I, bán kính IH.
Khi đó, đường tròn (I; IH) là đường tròn nội tiếp tam giác ABC cần vẽ.
b) Vì (I; r) nội tiếp tam giác ABC nên bán kính đường tròn nội tiếp tam giác ABC là:
\(r = \frac{{BC\sqrt 3 }}{6} = \frac{{4\sqrt 3 }}{6} = \frac{{2\sqrt 3 }}{3}\left( {cm} \right)\)