Câu hỏi/bài tập:
Cho tam giác ABC có các đường cao BE, CF. Biết rằng \(\widehat B = {60^o},\widehat C = {80^o}\).
a) Chứng tỏ rằng tứ giác BCEF nội tiếp một đường tròn có tâm là trung điểm của cạnh BC.
b) Tính số đo của các góc BFE và CEF.

a) + Chứng minh các tam giác BEC và tam giác BFC là các tam giác vuông.
+ Suy ra, các điểm B, F, E, C cùng thuộc đường tròn đường kính BC với tâm là trung điểm của BC.
b) Vì tứ giác BFEC nội tiếp đường tròn đường kính BC nên \(\widehat {FBC} + \widehat {FEC} = {180^o},\widehat {ECB} + \widehat {BFE} = {180^o}\), từ đó tính được các góc BFE và CEF.

Advertisements (Quảng cáo)
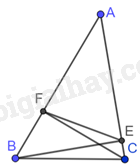
a) Vì BE, CF là các đường cao của tam giác ABC nên \(BE \bot AC,CF \bot AB\). Do đó, tam giác BFC vuông tại F và tam giác BEC vuông tại E.
Vì tam giác BFC vuông tại F nên ba điểm B, F, C thuộc đường tròn đường kính BC với tâm là trung điểm của BC.
Vì tam giác BEC vuông tại E nên ba điểm B, E, C thuộc đường tròn đường kính BC với tâm là trung điểm của BC.
Vậy tứ giác BCEF nội tiếp một đường tròn có tâm là trung điểm của cạnh BC.
b) Vì tứ giác BFEC nội tiếp đường tròn đường kính BC nên
+ \(\widehat {FBC} + \widehat {FEC} = {180^o}\), hay \(\widehat {FEC} = {180^o} - \widehat {FBC} = {180^o} - {60^o} = {120^o}\).
+ \(\widehat {ECB} + \widehat {BFE} = {180^o}\), hay \(\widehat {BFE} = {180^o} - \widehat {ECB} = {180^o} - {80^o} = {100^o}\).
