Gọi O là giao điểm của các đường trung trực của ba đoạn thẳng AB, AC, AD. Hướng dẫn trả lời Câu hỏi Thử thách nhỏ 1 trang 82 SGK Toán 9 Kết nối tri thức - Bài 29. Tứ giác nội tiếp.
Câu hỏi/bài tập:
Cho tứ giác ABCD, biết rằng các đường trung trực của ba đoạn thẳng AB, AC, AD đồng quy tại một điểm. Hãy giải thích vì sao ABCD là tứ giác nội tiếp.
+ Gọi O là giao điểm của các đường trung trực của ba đoạn thẳng AB, AC, AD.
+ Sử dụng tính chất đường trung trực chứng minh được \(OA = OB = OC = OD\).
+ Suy ra, bốn điểm A, B, C, D cùng thuộc một đường tròn. Vậy ABCD là tứ giác nội tiếp.
Advertisements (Quảng cáo)
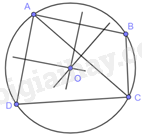
Gọi O là giao điểm của các đường trung trực của ba đoạn thẳng AB, AC, AD.
Vì O thuộc trung trực của AB nên \(OA = OB\).
Vì O thuộc trung trực của AC nên \(OA = OC\).
Vì O thuộc trung trực của AD nên \(OA = OD\).
Do đó, \(OA = OB = OC = OD\).
Suy ra, bốn điểm A, B, C, D cùng thuộc đường tròn (O). Vậy ABCD là tứ giác nội tiếp.