Câu hỏi/bài tập:
Cho một bát giác đều (đa giác đều 8 cạnh) nội tiếp một đường tròn tâm O (H.9.45). Hỏi mỗi góc của bát giác đều có số đo bằng bao nhiêu?

+ Gọi ABCDEFGH là bát giác đều nội tiếp đường tròn (O).
+ Chứng minh \(\Delta AOH = \Delta GOH = \Delta GOF = \Delta EOF = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.c.c} \right)\), suy ra: \(\widehat {HOA} = \widehat {HOG} = \widehat {GOF} = \widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \frac{{{{360}^o}}}{8} = {45^o}\)
+ Tính được: \(\widehat {OAB} = \widehat {OBA} = \frac{{{{180}^o} - \widehat {AOB}}}{2} = 67,{5^o}\)
+ Do đó \(\widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEF} = \widehat {EFG} = \widehat {FGH} = \widehat {GHA} = {135^o}\)

Advertisements (Quảng cáo)
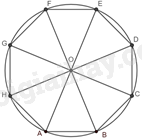
Gọi ABCDEFGH là bát giác đều nội tiếp đường tròn (O).
Vì ABCDEFGH là bát giác đều nên \(AB = BC = CD = DE = EF = FG = GH = HA\).
Vì ABCDEFGH là bát giác đều nội tiếp (O) nên \(OA = OB = OC = OD = OE = OF = OH = OG\).
Do đó, \(\Delta AOH = \Delta GOH = \Delta GOF = \Delta EOF = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.c.c} \right)\)
Suy ra: \(\widehat {HOA} = \widehat {HOG} = \widehat {GOF} = \widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \frac{{{{360}^o}}}{8} = {45^o}\)
Tam giác AOB cân tại O (do \(OA = OB\)) nên \(\widehat {OAB} = \widehat {OBA}\).Do đó, \(\widehat {OAB} = \widehat {OBA} = \frac{{{{180}^o} - \widehat {AOB}}}{2} = 67,{5^o}\)
Chứng minh tương tự ta có:
\(\widehat {OBC} = \widehat {OCB} = \widehat {ODE} = \widehat {OED} = \widehat {OEF} = \widehat {OFE} = \widehat {OFG} = \widehat {OGF} = \widehat {OGH} = \widehat {OHG} = \widehat {OHA} = \widehat {OAH} = 67,{5^o}\)
Suy ra \(\widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEF} = \widehat {EFG} = \widehat {FGH} = \widehat {GHA} = {135^o}\).
Vậy mỗi góc của bát giác đều bằng \({135^o}\).
