Hoạt động
Trả lời câu hỏi Hoạt động trang 85
Chứng minh rằng nếu một điểm thuộc đường tròn (O) thì:
a) Điểm đối xứng với nó qua tâm O cũng thuộc (O).
b) Điểm đối xứng với nó qua một đường thẳng d tùy ý đi qua O cũng thuộc (O).

a) Lấy điểm A bất kì thuộc (O).
Gọi A’ là điểm đối xứng với A qua O. Chứng minh OA = OA’ = R
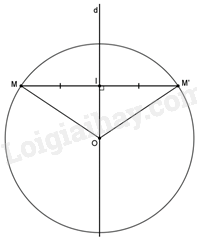
b) Lấy điểm M bất kì thuộc (O).
Gọi M’ là điểm đối xứng với M qua d. Chứng minh OM = OM’ = R

a) Lấy điểm A bất kì thuộc (O)
Gọi A’ là điểm đối xứng với A qua O.
Khi đó: O là trung điểm của AA’ hay OA = OA’ = R
⇒ A’ cũng thuộc đường tròn (O)
b) Lấy điểm M bất kì thuộc (O).
Gọi M’ là điểm đối xứng với M qua d.
Gọi I là giao điểm của d với MM’
Khi đó: MM’\( \bot \)OI tại M hay \(\widehat {OIM} = \widehat {OIM’} = 90^\circ \)
Xét tam giác OIM và tam giác OIM’ có:
Advertisements (Quảng cáo)
OI chung
\(\widehat {OIM} = \widehat {OIM’} = 90^\circ \)
IM = IM’
\( \Rightarrow \Delta OIM = \Delta OIM’\) (c.g.c)
Luyện tập2
Trả lời câu hỏi Luyện tập 2 trang 86
Cho đường tròn tâm O và hai điểm A, B thuộc (O). Gọi d là đường trung trực của đoạn AB. Chứng minh rằng d là một trục đối xứng của (O).

Chứng minh d đi qua tâm O.

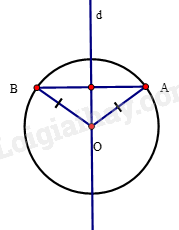
Vì OA = OB nên O thuộc d.
Vậy d là một trục đối xứng của (O).
Vận dụng2
Trả lời câu hỏi Vận dụng 2 trang 86
Trở lại tình huống mở đầu, bằng cách gấp mảnh giấy hình tròn theo hai cách khác nhau, Oanh có thể tìm được tâm của hình tròn. Em hãy làm thử xem.

Tình huống mở đầu: Bạn Oanh có một mảnh giấy hình tròn nhưng không còn dấu vết của tâm, Theo em, Oanh làm thế nào để tìm lại được tâm của hình tròn đó.
Khi gấp đôi hình tròn ta được đường kính, khi ta thực hiện 2 lần gấp như vậy theo 2 cách khác nhau ta được hai đường kính, mà hai đường kính sẽ giao nhau tại tâm của hình tròn. Từ đó ta xác định được tâm của hình tròn.

Gấp đôi hình tròn sao cho mép giấy của chúng đè khít lên nhau, ta miết phần ngăn cách hai nửa hình tròn ta được 1 đường kính, tiếp theo mở tờ giấy và gấp theo hướng khác, ta làm như vậy và xác định được đường kính mới, hai đường kính này cắt nhau tại tâm của hình tròn.
