Hoạt động3
Trả lời câu hỏi Hoạt động 3 trang 101
Cho điểm P ở bên ngoài một đường tròn tâm O. Hãy dùng thước và compa thực hiện các bước vẽ hình như sau:
- Vẽ đường tròn đường kính PO cắt đường tròn (O) tại A và B;
- Vẽ và chứng tỏ các đường thẳng PA và PB là hai tiếp tuyến của (O).

- Lấy trung điểm O’ của OP, vẽ đường tròn tâm O’ bán kính OO’.
- Ta chứng minh PA vuông góc với OA, PB vuông góc với OB.

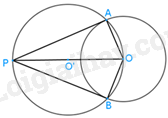
Tam giác OAP có O’A = O’O = O’P (cùng là bán kính của đường tròn (O’)) nên tam giác OAP vuông tại A.
Suy ra: PA\( \bot \)OA tại A hay PA là tiếp tuyến của đường tròn (O’)
Tam giác OBP có O’B = O’O = O’P (cùng là bán kính của đường tròn (O’)) nên tam giác OAP vuông tại B.
Suy ra: PB\( \bot \)OB tại B hay PB là tiếp tuyến của đường tròn (O’)
Hoạt động4
Trả lời câu hỏi Hoạt động 4 trang 102
(Dựa vào hình vẽ có được sau HĐ3).

Bằng cách xét hai tam giác OPA và OPB, chứng minh rằng:
a) PA = PB;
b) PO là tia phân giác của góc APB;
c) OP là tia phân giác của góc AOB.

Advertisements (Quảng cáo)
Chứng minh \(\Delta {\rm{OAP}} = \Delta {\rm{OBP}}\), từ đó suy ra các cặp cạnh, góc tương ứng bằng nhau.

a) Xét hai tam giác vuông OAP và OBP có:
OA = OB
OP chung
Vậy \(\Delta {\rm{OAP}} = \Delta {\rm{OBP}}\) (cạnh huyền – cạnh góc vuông)
Suy ra: PA = PB (hai cạnh tương ứng)
b) Vì \(\Delta {\rm{OAP}} = \Delta {\rm{OBP}}\) (câu a) nên \(\widehat {{\rm{OAP}}} = \widehat {{\rm{OBP}}}\) (hai góc tương ứng)
Suy ra PO là tia phân giác của góc APB.
c) Vì \(\Delta {\rm{OAP}} = \Delta {\rm{OBP}}\) (câu a) nên \(\widehat {{\rm{AOP}}} = \widehat {{\rm{BOP}}}\) (hai góc tương ứng)
Suy ra OP là tia phân giác của góc AOB.
Thử thách nhỏ
Trả lời câu hỏi Thử thách nhỏ trang 103
Cho góc xPy và điểm A thuộc tia Px. Hãy vẽ đường tròn tâm O tiếp xúc với cả hai cạnh của góc xPy sao cho A là một trong hai tiếp điểm.

Cần nhớ kiến thức đường phân giác: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đấy.
Đường tròn tiếp xúc với đường thẳng thì khoảng cách từ tâm đến đường thẳng bằng bán kính

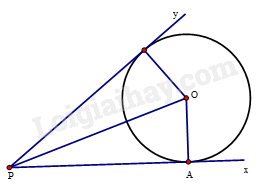
Vẽ góc xPy rồi lấy điểm A trên Px, để vẽ đường tròn tâm O tiếp xúc với cả hai cạnh của góc xPy thì khoảng cách từ O đến hai tia Px và Py bằng nhau và bằng bán kính của đường tròn nên O thuộc đường phân giác của góc xPy.
Để (O) tiếp xúc với Px tại A thì OA vuông góc với Px tại A.
Do đó O là giao điểm của phân giác góc xPy và đường vuông góc với Px tại A.
