
Trên mặt phẳng tọa độ Oxy, hãy xác định vị trí tương đối của mỗi điểm \(M( - 1;1),N(\sqrt 2 ; - \sqrt 2 ),P(1; - 2)\) đối với đường tròn (O;2).
Cho đường tròn \(\left( {O;R} \right)\) và điểm M.
+) Nếu \(OM < R \Rightarrow \) Điểm M nằm bên trong đường tròn.
+) Nếu \(OM = R \Rightarrow \) Điểm M nằm trên đường tròn.
+) Nếu \(OM > R \Rightarrow \) Điểm M nằm bên ngoài đường tròn.

Advertisements (Quảng cáo)
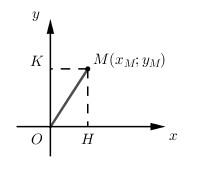
Cho điểm \(M\left( {x;y} \right)\). Gọi H, K lần lượt là hình chiếu của M trên Ox và Oy, khi đó ta có \(OH = \left| {{x_M}} \right|;\,\,OK = \left| {{y_M}} \right|\).
Do OHMK là hình chữ nhật (Tứ giác có 3 góc vuông) \( \Rightarrow MH = OK = \left| {{y_M}} \right|\).
Áp dụng định lí Pytago trong tam giác vuông OMH có:
\(O{M^2} = \sqrt {O{H^2} + H{M^2}} \)\(\, = \sqrt {{{\left| {{x_M}} \right|}^2} + {{\left| {{y_M}} \right|}^2}} = \sqrt {x_M^2 + y_M^2} \).
Áp dụng công thức trên ta tính được:
\(\begin{array}{l}OM = \sqrt {{{\left( { - 1} \right)}^2} + {1^2}} = \sqrt 2 \\ON = \sqrt {{{\left( {\sqrt 2 } \right)}^2} + {{\left( { - \sqrt 2 } \right)}^2}} = \sqrt 4 = 2\\OP = \sqrt {{1^2} + {{\left( { - 2} \right)}^2}} = \sqrt 5 \end{array}\)
+) Vì \(OM < R\,\,\left( {\sqrt 2 < 2} \right) \Rightarrow \) Điểm M nằm bên trong \(\left( {O;2} \right)\).
+) Vì \(ON = R\,\,\left( {2 = 2} \right) \Rightarrow \) Điểm N nằm trên \(\left( {O;2} \right)\).
+) Vì \(OP > R\,\,\left( {\sqrt 5 > 2} \right) \Rightarrow \) Điểm P nằm bên ngoài \(\left( {O;2} \right)\).
