
Cho hai hàm số y = x và y = 3x.
a) Vẽ đồ thị của hai hàm số trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm A, B của hai đồ thị trên lần lượt với đồ thị của hàm số y = 3.
+) Cách vẽ đồ thị hàm số bậc nhất \(y = ax + b,\,\,\left( {a \ne 0} \right)\)
Tìm tọa độ giao điểm của đồ thị hàm số \(y = ax + b\)với trục tung là \(A\left( {0;b} \right)\) và trục hoành \(B\left( { - \dfrac{b}{a};0} \right)\) .
Đồ thị hàm số cần tìm là đường thẳng đi qua 2 điểm A, B
+) Muốn tìm tọa độ giao điểm của hai đồ thị hàm số \(y = f\left( x \right);y = g\left( x \right)\) ta làm như sau:
Viết phương trình hoành độ giao điểm của 2 hàm số: \(f\left( x \right) = g\left( x \right) \Rightarrow x = ? \Rightarrow y = \) . từ đó ta tìm được tọa độ giao điểm của 2 đồ thị.

Cho hai hàm số y = x và y = 3x.
a) Vẽ đồ thị của hai hàm số trên cùng một mặt phẳng tọa độ.
+) y = x
Bảng giá trị
|
x |
0 |
1 |
|
y |
Advertisements (Quảng cáo) 0 |
1 |
Đồ thị hàm số y = x là đường thẳng đi qua hai điểm O(0;0); C(1;1)
+) y = 3x
Bảng giá trị
|
x |
0 |
1 |
|
y |
0 |
3 |
Đồ thị hàm số y = 3x là đường thẳng đi qua hai điểm O(0;0); B(1;3)
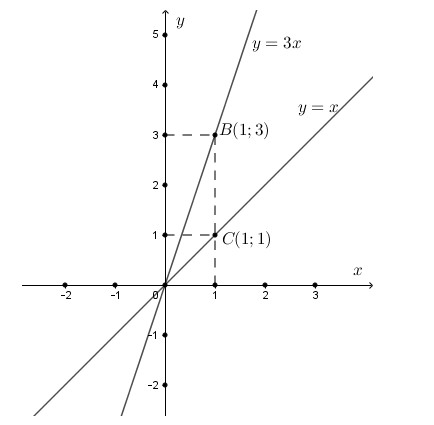
b) Tìm tọa độ giao điểm A, B của hai đồ thị trên lần lượt với đồ thị của hàm số y = 3.
+) Phương trình hoành độ giao điểm của đồ thị y = x và đồ thị hàm số y = 3 là:
x = 3
Khi đó tọa độ giao điểm của đồ thị y = x và đồ thị y = 3 là A(3;3)
+) Phương trình hoành độ giao điểm của đồ thị y = 3x và đồ thị hàm số y = 3 là:
3x = 3. Suy ra x = 1
Khi đó tọa độ giao điểm của đồ thị y = 3x và đồ thị y = 3 là B(1;3)
