1. Khái niệm tỉ số lượng giác của một góc nhọn - Hoạt động 2 trang 78 Tài liệu dạy – học Toán 9 tập 1. Giải bài tập Vẽ góc nhọn
Vẽ góc nhọn \(\widehat {mOn} = x\). Lấy hai điểm B và B’ trên Om. Gọi A và A’ là hình chiếu vuông góc của B và B’ trên On.
- Hãy chứng minh hai tam giác sau luôn đồng dạng : OAB và OA’B’.
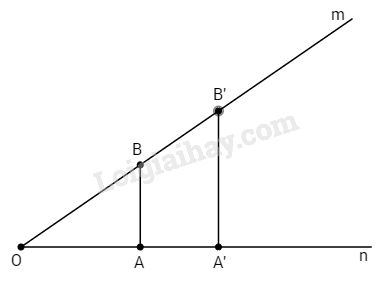
Xét tam giác OAB và OA’B’ có:
+) \(\widehat O\) chung;
Advertisements (Quảng cáo)
+) \(\widehat {OAB} = \widehat {OA’B’} = {90^o}\)
\( \Rightarrow \) Tam giác OAB đồng dạng với tam giác OA’B’ (g.g)
- So sánh các cặp tỉ số :
- \(\dfrac{{AB}}{{OA}};\dfrac{{A’B’}}{{OA’}}\)\(\dfrac{{AB}}{{OA}} = \dfrac{{A’B’}}{{OA’}}\)
- \(\dfrac{{AB}}{{OB}};\dfrac{{A’B’}}{{OB’}}\)\(\dfrac{{AB}}{{OB}} = \dfrac{{A’B’}}{{OB’}}\)
- \(\dfrac{{OA}}{{OB}};\dfrac{{OA’}}{{OB’}}\)\(\dfrac{{OA}}{{OB}} = \dfrac{{OA’}}{{OB’}}\)