
Trên đường tròn (O) lấy hai điểm A, B. Hai tiếp tuyến tại A và B cắt nhau tại M (xem hình bên). Hãy chứng minh AB vuông góc với OM rồi so sánh các góc \(\widehat {BAM},\widehat {AOM},\widehat {BOM}\).
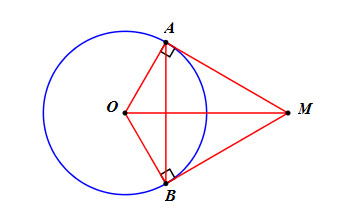

Ta có \(OA = OB = R \Rightarrow O\) thuộc trung trực của AB
\(MA = MB\) (tính chất hai tiếp tuyến cắt nhau) \( \Rightarrow M\) thuộc trung trực của AB.
Từ đó suy ra OM là đường trung trực của AB \( \Rightarrow OM \bot AB\).
Gọi \(H = OM \cap AB\) ta có:
Advertisements (Quảng cáo)
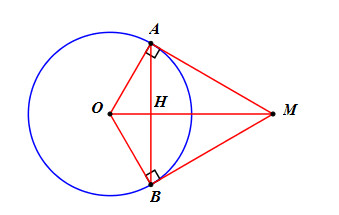
\(\widehat {BAM} + \widehat {AOB} = \widehat {AOM} = {90^0}\) (do AM là tiếp tuyến của (O) nên \(AM \bot OA\))
Tam giác OAH vuông tại H nên \(\widehat {AOM} + \widehat {AOB} = {90^0}\) (hai góc nhọn trong tam giác vuông thì phụ nhau).
\( \Rightarrow \widehat {BAM} = \widehat {AOM}\).
Lại có \(\widehat {AOM} = \widehat {BOM}\) (tính chất hai tiếp tuyến cắt nhau).
Vậy \(\widehat {BAM} = \widehat {AOM} = \widehat {BOM}\) (đpcm).
