2. Góc tạo bởi tia tiếp tuyến và dây cung - Thử tài bạn 3 trang 86 Tài liệu dạy – học Toán 9 tập 2. Giải bài tập Cho tam giác ABC vuông cân tại A và nội tiếp đường tròn (O). Vẽ tiếp tuyến Au với đường tròn

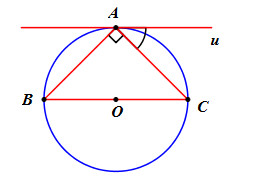
Cho tam giác ABC vuông cân tại A và nội tiếp đường tròn (O). Vẽ tiếp tuyến Au với đường tròn (O) như trong hình. Hãy tính số đo \(\widehat {CAu}\) .

Advertisements (Quảng cáo)
Ta có: \(\widehat {CAu}\) là góc tạo bởi tia tiếp tuyến và dây cung chắn cung AC .
\(\widehat {AOC}\) là góc ở tâm chắn cung AC.
Vì tam giác ABC cân tại A nên trung tuyến AM đồng thời là đường cao \( \Rightarrow AO \bot BC \Rightarrow \widehat {AOC} = {90^0} \Rightarrow sd\,cung\,AC = {90^0}\).
Vậy \(\widehat {CAu} = \dfrac{1}{2}sd\,cung\,AC = \dfrac{1}{2}{.90^0} = {45^0}\).
