3. Đường tròn nội tiếp - Hoạt động 4 trang 100 Tài liệu dạy – học Toán 9 tập 2. Giải bài tập Cho hình vuông ABCD cạnh a. Gọi O là giao điểm của hai đường chéo. Đường tròn tâm O bán
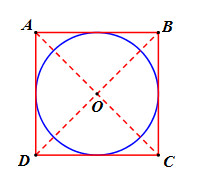
Cho hình vuông ABCD cạnh a. Gọi O là giao điểm của hai đường chéo. Đường tròn tâm O bán kính \(\dfrac{a}{2}\) có tiếp xúc với các cạnh của hình vuông hay không?
Advertisements (Quảng cáo)
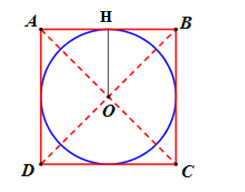
Kẻ \(OH \bot AB\) ta có: \(\Delta OHA\) vuông tại H có \(\widehat {OAH} = {45^0} \Rightarrow \Delta OAH\) vuông cân tại O \( \Rightarrow OH = AH\).
Xét tam giác OAB cân tại O có OH là đường cao đồng thời là trung tuyến \( \Rightarrow AH = BH = \dfrac{{AB}}{2} = \dfrac{a}{2}\).
\( \Rightarrow OH = \dfrac{a}{2}\). Hoàn toàn tương tự ta chứng minh được điểm O cách đều các cạnh BC, CD, DA một khoảng \(\dfrac{a}{2}\).
Vậy đường tròn tâm O bán kính \(\dfrac{a}{2}\) tiếp xúc với các cạnh của hình vuông.