2. Dấu hiệu nhận biết tiếp tuyến của đường tròn - Hoạt động 6 trang 136 Tài liệu dạy – học Toán 9 tập 1. Giải bài tập Gọi I là giao điểm ba đường phân giác trong tam giác ABC.
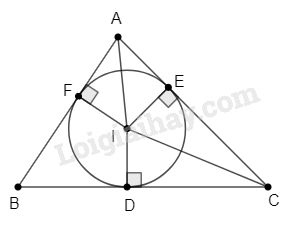
Gọi I là giao điểm ba đường phân giác trong tam giác ABC. Vẽ ID, IE, IF lần lượt vuông góc với BC, AC và AB.
a) Chứng minh rằng IE = IF.
b) Chứng minh rằng IE = ID. Suy ra ba điểm D, E và F cùng nằm trên đường tròn (I ; ID)
a) Xét tam giác vuông AIE và AIF có:
Advertisements (Quảng cáo)
AI chung;
\(\widehat {IAE} = \widehat {IAF}\,\,\left( {gt} \right)\)
\( \Rightarrow \Delta AIE = \Delta AIF\) (cạnh huyền – góc nhọn)
\(IE = IF\) (2 cạnh tương ứng)
b) Chứng minh tương tự ta có \(\Delta CID = \Delta CIE\) (cạnh huyền – góc nhọn) \( \Rightarrow IE = ID\)
Vậy \(IE = IF = ID \Rightarrow \) ba điểm E, F, D cùng thuộc \(\left( {I;ID} \right)\).
Baitapsgk.com