4. Tỉ số lượng giác của các góc đặc biệt - Hoạt động 7 trang 82 Tài liệu dạy – học Toán 9 tập 1. Giải bài tập Cho tam giác vuông cân có cạnh bằng 1 m. Tính độ dài cạnh huyền rồi dùng kết quả đó để tính

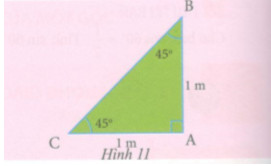
Cho tam giác vuông cân có cạnh bằng 1 m. Tính độ dài cạnh huyền rồi dùng kết quả đó để tính các tỉ số lượng giác của góc \({45^o}\).

Áp dụng định lý Pythagore vào tam giác ABC vuông tại A có:
Advertisements (Quảng cáo)
\(B{C^2} = A{B^2} + A{C^2} \\\Rightarrow BC = \sqrt {A{B^2} + A{C^2}} = \sqrt 2 \,\,m\)
Xét tam giác ABC vuông tại A có:
\(\begin{array}{l}\sin {45^o} = \dfrac{{AC}}{{BC}} = \dfrac{{\sqrt 2 }}{2}\\\cos {45^o} = \dfrac{{AB}}{{BC}} = \dfrac{{\sqrt 2 }}{2}\\\tan {45^o} = \dfrac{{AC}}{{AB}} = 1\\\cot {45^o} = \dfrac{{AB}}{{AC}} = 1\end{array}\)
