Cho đường tròn tâm O có bán kính OA=R, dây BC vuông góc với OA tại trung điểm M của OA.. Bài 25 trang 111 sgk Toán 9 - tập 1 - Bài 5. Dấu hiệu nhận biết tiếp tuyến của đường tròn
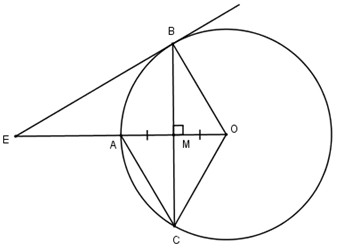
Cho đường tròn tâm O có bán kính OA=R, dây BC vuông góc với OA tại trung điểm M của OA.
a) Từ giác OCAB là hình gì? Vì sao?
b) Kẻ tiếp tuyến với đường tròn tại B, nó cắt đường thẳng OA tại E. Tính độ dài BE theo R.
Hướng dẫn giải:
a) Ta có \(OA\perp BC\Rightarrow MB=MC\).
Mặt khác:
Advertisements (Quảng cáo)
\(MA=MO\) nên tứ giác ABOC là hình bình hành.
Hình bình hành này có hai đường chéo vuông góc nên là hình thoi.
b) Ta có \(BA=BO\) (hai cạnh hình thoi) mà \(BO=OA\) (bán kính) nên tam giác ABO là tam giác đều.
Suy ra \(\widehat{BOA}=60^{\circ}\).
Ta có EB là tiếp tuyến \(\Rightarrow EB\perp OB\).
Xét tam giác BOE vuông tại B, có:
\(BE=BO\cdot tg60^{\circ}= R.tg60^0=R\sqrt{3}.\)