5. a) Vẽ đồ thị hàm số y = x và y =2x trên cùng một mặt phẳng tọa độ Oxy (h.5).
b) Đường thẳng song song với trục Ox và cắt trục Oy tại điểm có tung độ Y = 4 lần lượt cắt các đường thẳng y = 2x, y = x tại hai điểm A và B.
Tìm tọa độ của các điểm A, B và tính chu vi, diện tích của tam giác OAB theo đơn vị đo trên các trục tọa độ là xentimét.
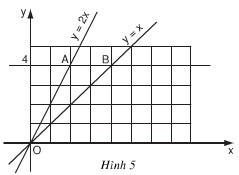

a) Xem hình trên và vẽ lại
b) A(2; 4), B(4; 4).
Advertisements (Quảng cáo)
Tính chu vi ∆OAB.
Dễ thấy AB = 4 - 2 = 2 (cm).
Áp dụng định lý Py-ta-go, ta có:
\(\eqalign{
& OA = \sqrt {{2^2} + {4^2}} = 2\sqrt 5 \left( {cm} \right) \cr
& OB = \sqrt {{4^2} + {4^2}} = 4\sqrt 2 \left( {cm} \right) \cr} \)
Tính diện tích ∆OAB.
Gọi C là điểm biểu diễn số 4 trên trục tung, ta có:
\(\eqalign{
& {S_{\Delta OAB}} = {S_{\Delta OBC}} - {S_{\Delta OAC}} \cr
& = {1 \over 2}OC.OB - {1 \over 2}OC.AC \cr
& = {1 \over 2}{.4^2} - {1 \over 2}.4.2 = 8 - 4 = 4\left( {c{m^2}} \right) \cr} \)
