Bài 83 trang 99 sgk Toán 9 tập 2,Vẽ hình 62...

Bài 83. a) Vẽ hình 62 (tạo bởi các cung tròn) với $HI = 10cm$ và $HO = 2cm$. Nêu cách vẽ.

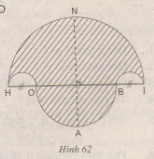
b) Tính diện tích hình $HOABINH$ (miền gạch sọc)

c) Chứng tỏ rằng hình tròn đường kính $NA$ có cùng diện tích với hình $HOABINH$ đó.

Hướng dẫn giải:

a) Vẽ nửa đường tròn đường kính $HI = 10 cm$, tâm $M$

Trên đường kính $HI$ lấy điểm $O$ và điểm $B$ sao cho $HO = BI = 2cm$.

Vẽ hai nửa đường tròn đường kính $HO$, $BI$ nằm cùng phía với đường tròn $(M)$.

vẽ nửa đường tròn đường kính $OB$ nằm khác phía đối với đường tròn $(M)$. Đường thẳng vuông góc với $HI$ tại $M$ cắt $(M)$ tại $N$ và cắt đường tròn đường kính $OB$ tại $A$.

b)  Diện tích hình $HOABINH$ là:

$\frac{1}{2}$.$π.5^2$ + $\frac{1}{2}$.$π.3^2$ – $π.1^2$ = $\frac{25}{2}π$ + $\frac{9}{2}π$ - $π$ = $16π$ ($cm^2$) (1)

c) Diện tích hình tròn đường kính $NA$ bằng:

             $π. 4^2 = 16π$  ($cm^2$)                                           (2)

So sánh (1) và (2) ta thấy hình tròn đường kính $NA$ có cùng diện tích với hình $HOABINH$