Câu hỏi/bài tập:

Cho tam giác ABC nội tiếp đường tròn (O). Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB. Chứng minh rằng các tứ giác ANOP, BPOM, CMON là các tứ giác nội tiếp

+ Chứng minh OP, ON, OM lần lượt là các đường cao của các tam giác AOB, AOC, BOC.
+ Tứ giác ANOP có \(\widehat {ANO} = \widehat {APO} = {90^0}\) nên tứ giác ANOP nội tiếp đường tròn có tâm là trung điểm của AO và bán kính bằng \(\frac{{AO}}{2}\).
Advertisements (Quảng cáo)
+ Chứng minh tương tự ta có BPOM, CMON cũng là các tứ giác nội tiếp.

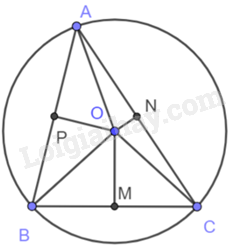
Do các tam giác AOB, AOC, BOC đều cân tại O nên OP, ON, OM lần lượt là các đường cao của các tam giác này.
Do vậy, tứ giác ANOP có \(\widehat {ANO} = \widehat {APO} = {90^0}\). Do vậy tứ giác ANOP nội tiếp đường tròn có tâm là trung điểm của AO và bán kính bằng \(\frac{{AO}}{2}\). Tương tự BPOM, CMON cũng là các tứ giác nội tiếp.
