Câu hỏi/bài tập:

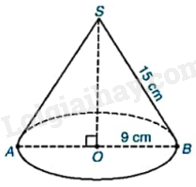
Cho hình nón có bán kính đáy bằng 9cm, độ dài đường sinh bằng 15cm.
a) Tính diện tích xung quanh của hình nón.
b) Tính thể tích của hình nón.
c) Diện tích toàn phần của hình nón bằng tổng diện tích xung quanh và diện tích đáy. Tính diện tích toàn phần của hình nón đã cho.

a) Diện tích xung quanh của hình nón bán kính đáy r và độ dài đường sinh l là: \({S_{xq}} = \pi rl\).
b) Thể tích của hình nón bán kính đáy r và chiều cao h là: \(V = \frac{1}{3}\pi {r^2}h\).
c) + Diện tích đáy hình nón là: \(S = \pi {r^2}\).
Advertisements (Quảng cáo)
+ Diện tích toàn phần của hình nón bằng tổng diện tích xung quanh và diện tích đáy.

a) Diện tích xung quanh của hình nón là:
\({S_{xq}} = \pi .Rl = 9.15.\pi = 135\pi \left( {c{m^2}} \right)\).
b) Chiều cao của hình nón là:
\(h = \sqrt {{l^2} - {R^2}} = \sqrt {{{15}^2} - {9^2}} = 12\left( {cm} \right)\).
Thể tích của hình nón là:
\(V = \frac{1}{3}\pi .{R^2}h = \frac{1}{3}\pi {.9^2}.12 = 324\pi \left( {c{m^3}} \right)\).
c) Diện tích toàn phần của hình nón là:
${{S}_{tp}}={{S}_{xq}}+{{S}_{đáy}}=\pi Rl+\pi {{R}^{2}}=\pi R\left( l+R \right)\\=\pi .9.\left( 15+9 \right)=216\pi \left( c{{m}^{2}} \right)$
