Câu hỏi/bài tập:

Từ một tấm tôn hình chữ nhật có kích thước \(50cm \times 240cm\), người ta làm các thùng đựng nước hình trụ có chiều cao bằng 50cm, theo hai cách sau:
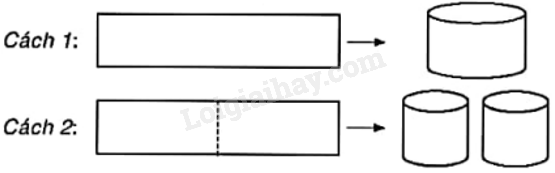
Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng nước hình trụ.
Cách 2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau hình chữ nhật, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.
Kí hiệu \({V_1}\) là thể tích của thùng gò được theo Cách 1và \({V_2}\) là tổng thể tích của hai thùng gò được theo Cách 2. Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}\) (giả sử các mối hàn là không đáng kể).

Advertisements (Quảng cáo)
+ Nếu làm theo cách 1 thì chu vi đường tròn đáy là: 240cm; \({R_1} = \frac{{240}}{{2\pi }}\).
+ Nếu làm theo cách 2 thì chu vi đường tròn đáy bằng 120cm, \({R_2} = \frac{{120}}{{2\pi }}\).
+ Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}\).

Nếu làm theo cách 1 thì chu vi đường tròn đáy là: 240cm; \({R_1} = \frac{{240}}{{2\pi }} = \frac{{120}}{\pi }\left( {cm} \right)\).
Nếu làm theo cách 2 thì chu vi của mỗi đường tròn đáy bằng 120cm, \({R_2} = \frac{{120}}{{2\pi }} = \frac{{60}}{\pi }\left( {cm} \right)\).
Ta có: \(\frac{{{V_1}}}{{{V_2}}} = \frac{{\pi R_1^2h}}{{2\pi R_2^2h}}= \frac{{R_1^2}}{{2R_2^2}} = \frac{1}{2}{\left( {\frac{{{R_1}}}{{{R_2}}}} \right)^2}\)
\(= \frac{1}{2} \cdot {\left( {\frac{{120}}{\pi }:\frac{{60}}{\pi }} \right)^2} = 2\).
