Câu hỏi/bài tập:

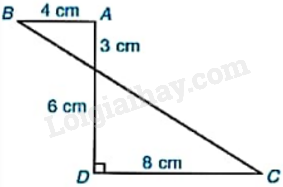
Tính thể tích của hình tạo thành khi cho hình ABCD quay quanh AD một vòng.

Thể tích của hình nón bán kính r và chiều cao h là: \(V = \frac{1}{3}\pi {r^2}h\).
Advertisements (Quảng cáo)

Hình tạo thành là hai hình nón. Hình nón 1 có: \({R_1} = 8{\rm{\;cm}},{h_1} = 6{\rm{\;cm}}\); hình nón 2 có: \({R_2} = 4{\rm{\;cm}},{h_2} = 3{\rm{\;cm}}\).
Thể tích của hình nón 1 là: \({V_1} = \frac{1}{3}\pi R_1^2{h_1} = \frac{1}{3}\pi \cdot {8^2} \cdot 6 = 128\pi \;\,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Thể tích của hình nón 2 là: \({V_2} = \frac{1}{3}\pi {R_2}{\;^2}{h_2} = \frac{1}{3}\pi \cdot {4^2} \cdot 3 = 16\pi \;\,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Thể tích hình tạo thành là: \(V = {V_1} + {V_2} = 128\pi + 16\pi = 144\pi \,\,\;\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
