Giải bài 22 trang 31 SBT toán 10 - Cánh diều - Bài tập cuối chương II
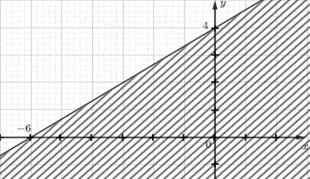
Phần không bị gạch (kể cả d) ở Hình 11 là miền nghiệm của bất phương trình:
|
A. \(2x - 3y \le - 12\) B. \(2x - 3y \ge - 12\) C. \(3x - 2y \le 12\) D. \(3x - 2y \ge 12\) |
 |
|
|
Hình 11 |
|
|
|
Advertisements (Quảng cáo)
Xác định phương trình của đường thẳng
Xét điểm thuộc miền nghiệm và kết luận
Gọi đường thẳng d có dạng: y = ax + b
d đi qua (-6;0) và (0;4) nên ta có: \(\left\{ \begin{array}{l}0 = - 6a + b\\4 = 0.a + b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{2}{3}\\b = 4\end{array} \right. \Leftrightarrow y = \frac{2}{3}x + 4 \Leftrightarrow 2x - 3y = - 12\)
Lấy điểm O(0; 0) không thuộc d, ta có 2.0 – 3.0 = 0 > – 12, mà điểm O không thuộc miền nghiệm
Do đó bất phương trình cần tìm là \(2x - 3y \le - 12\)
Chọn A