
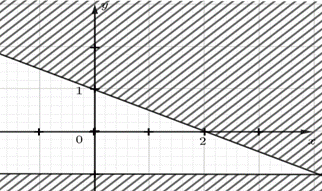
Phần không bị gạch (kể cả tia AB, AC) ở Hình 12 là miền nghiệm của hệ bất phương trình:
|
A. \(\left\{ {\begin{array}{*{20}{c}}{x + 2y \ge 2}\\{y \ge - 1}\end{array}} \right.\) B. \(\left\{ {\begin{array}{*{20}{c}}{x + 2y \le 2}\\{y \ge - 1}\end{array}} \right.\) C. \(\left\{ {\begin{array}{*{20}{c}}{2x + y < 2}\\{y > - 1}\end{array}} \right.\) D. \(\left\{ {\begin{array}{*{20}{c}}{2x + y > 2}\\{y \ge - 1}\end{array}} \right.\) |
 |
|
|
Hình 12 |

Tìm phương trình của hai đường thẳng trong hình vé
Xét điểm thuộc miền nghiệm và kết luận
Advertisements (Quảng cáo)

Gọi d là đường thẳng đi qua hai điểm A và B, vì đường thẳng này cắt hai trục tọa độ Ox, Oy lần lượt tại các điểm có tọa độ là (2; 0) và (0; 1) nên có phương trình là: \(\frac{x}{2} + \frac{y}{2} = 1 \Leftrightarrow x + 2y = 2\)
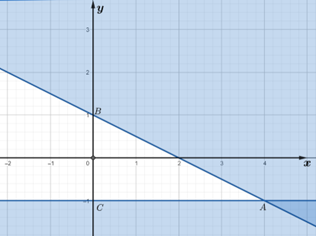
Lấy O(0; 0) có 0 + 2.0 = 0 < 2 và điểm O thuộc miền nghiệm của hệ bất phương trình và miền nghiệm kể cả đường thẳng d nên ta có bất phương trình x + 2y ≤ 2 (1).
Gọi d’ là đường thẳng đi qua hai điểm A và C và song song với trục hoành Ox nên có phương trình y = – 1.
Lấy điểm O(0; 0) có 0 > – 1 và điểm O thuộc miền nghiệm của hệ bất phương trình và miền nghiệm kể cả đường thẳng d nên ta có bất phương trình y ≥ – 1 (2).
Từ (1) và (2) ta có hệ bất phương trình: \(\left\{ {\begin{array}{*{20}{c}}{x + 2y \le 2}\\{y \ge - 1}\end{array}} \right.\)
Chọn B
