
Biểu diễn miền nghiệm của các hệ bất phương trình sau:
a) \(\left\{ {\begin{array}{*{20}{c}}{x - 3y < 0}\\{x + 2y > - 3}\\{x + y < 2}\end{array}} \right.\) b) \(\left\{ {\begin{array}{*{20}{c}}{x - 2y \le 3}\\{3x + 2y \ge 9}\\{x + y \le 6}\\{x \ge 1}\end{array}} \right.\) c) \(\left\{ {\begin{array}{*{20}{c}}{x + 2y \le 2}\\{x + 2y \ge - 2}\\{x - 2y \le 2}\\{x - 2y \ge - 2}\end{array}} \right.\)

Xác định miền nghiệm của từng bpt. Miền nghiệm của hệ bpt là miền giao của các miền nghiệm ấy.
Biểu diễn miền nghiệm của bpt \(ax + by < c\)
Bước 1: Vẽ đường thẳng \(d:ax + by = c\)
Bước 2: Lấy một điểm \(M\left( {{x_o};{y_o}} \right)\) không thuộc d (ta thường lấy gốc tọa độ O nếu \(c \ne 0\)). Tính \(a{x_o} + b{y_o}\) và so sánh với c
Bước 3: Kết luận
Nếu \(a{x_o} + b{y_o} < c\)thì nửa mặt phẳng (không kể đường thẳng d) chứa điểm M là miền nghiệm của bất phương trình \(ax + by < c\)
Nếu \(a{x_o} + b{y_o} > c\) thì nửa mặt phẳng (không kể d) không chứa điểm M là miền nghiệm của bất phương trình \(ax + by > c\)

a) Vẽ các đường thẳng:
\({d_1}{\rm{:}}\;x-3y = 0\) đi qua hai điểm có tọa độ (0; 0) và (3; 1).
\({d_2}{\rm{:}}\;x + 2y = - 3\) đi qua hai điểm có tọa độ (– 3; 0) và (1; – 2).
\({d_3}{\rm{:}}\;x + y = 2\) đi qua hai điểm có tọa độ (2; 0) và (0; 2).
Xét điểm A(1;0), không thuộc \({d_1},{d_2},{d_3}.\)
\(1 - 3.0 = 1 > 0 \Rightarrow A(1;0)\) không thuộc miền nghiệm của BPT \(x - 3y < 0\)
\(1 + 2.0 = 1 > - 3 \Rightarrow A(1;0)\) thuộc miền nghiệm của BPT \(x + 2y > - 3\)
\(1 + 0 = 1 < 2 \Rightarrow A(1;0)\) thuộc miền nghiệm của BPT \(x + y < 2\)
Biểu diễn miền nghiệm của từng bpt và gạch bỏ các miền không là nghiệm, ta được:
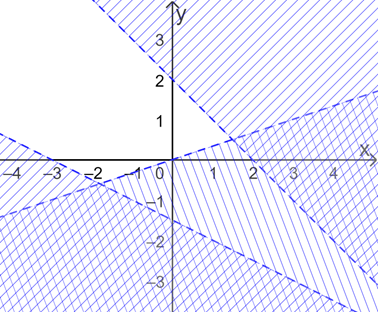
Miền nghiệm của hệ bpt là miền không gạch (không kể các bờ) trong hình trên.
b) Vẽ các đường thẳng:
d1: x – 2y = 3 đi qua hai điểm có tọa độ là (3; 0) và (1; – 1).
Advertisements (Quảng cáo)
d2: 3x + 2y = 9 đi qua hai điểm (3; 0) và (1; 3).
d3: x + y = 6 đi qua hai điểm (6; 0) và (0; 6).
d4: x = 1 song song với trục tung và đi qua điểm (1; 0).
Xét điểm O(0;0), không thuộc \({d_1},{d_2},{d_3},{d_4}.\)
\(0 - 2.0 = 0 \le 3 \Rightarrow O(0;0)\) thuộc miền nghiệm của BPT \(x - 2y \le 3\)
\(3.0 + 2.0 < 9 \Rightarrow O(0;0)\) không thuộc miền nghiệm của BPT \(3x + 2y \ge 9\)
\(0 + 0 = 0 \le 6 \Rightarrow O(0;0)\) thuộc miền nghiệm của BPT \(x + y \le 6\)
\(0 < 1 \Rightarrow O(0;0)\) không thuộc miền nghiệm của BPT \(x \ge 1\)
Biểu diễn miền nghiệm của từng bpt và gạch bỏ các miền không là nghiệm, ta được:
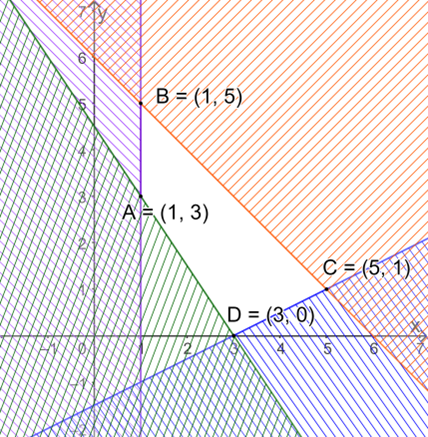
Miền nghiệm của hệ BPT là miền tứ giác ABCD (kể cả các cạnh) với A(1;3), B(1;5), C(5;1), D(3;0).
c) Vẽ các đường thẳng:
d1: x + 2y = 2 đi qua hai điểm có tọa độ là (2; 0) và (0; 1).
d2: x + 2y = – 2 đi qua hai điểm có tọa độ là (– 2; 0) và (0; – 1).
d3: x – 2y = 2 đi qua hai điểm có tọa độ là (2; 0) và (0; – 1).
d4: x – 2y = – 2 đi qua hai điểm có tọa độ là (–2; 0) và (0; 1).
Xét điểm O(0;0), không thuộc \({d_1},{d_2},{d_3},{d_4}.\)
\(0 + 2.0 = 0 \le 2 \Rightarrow O(0;0)\) thuộc miền nghiệm của BPT \(x + 2y \le 2\)
\(0 + 2.0 = 0 \ge - 2 \Rightarrow O(0;0)\) thuộc miền nghiệm của BPT \(x + 2y \ge - 2\)
\(0 - 2.0 = 0 \le 2 \Rightarrow O(0;0)\) thuộc miền nghiệm của BPT \(x - 2y \le 2\)
\(0 - 2.0 = 0 \ge - 2 \Rightarrow O(0;0)\) thuộc miền nghiệm của BPT \(x - 2y \ge - 2\)
Như vậy O(0;0) thuộc miền nghiệm của hệ bpt.
Biểu diễn miền nghiệm của từng bpt và gạch bỏ các miền không là nghiệm, ta được:
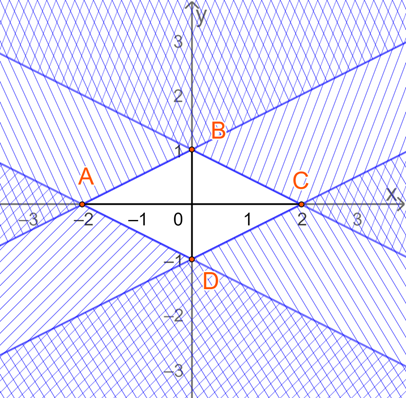
Miền nghiệm của hệ BPT là miền tứ giác ABCD (kể cả các cạnh) với A(-2;0), B(0;1), C(2;0), D(0;-1).
