
Hình 13 mô tả sơ đồ một sân khấu gắn với hệ trục tọa độ Oxy (đơn vị trên các trục tọa độ là 1 mét). Phần thính phòng giới hạn bởi hai đường thẳng d1 và d2 là vị trí ngồi của khán giả có thể nhìn thấy dàn hợp xướng. Gọi (x; y) là tọa độ ngồi của khán giả ở thính phòng. Viết hệ bất phương trình bậc nhất hai ẩn x, y mà khán giả có thể nhìn thấy dàn hợp xướng.
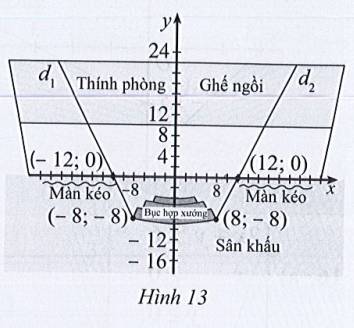

Ta có hình vẽ sau
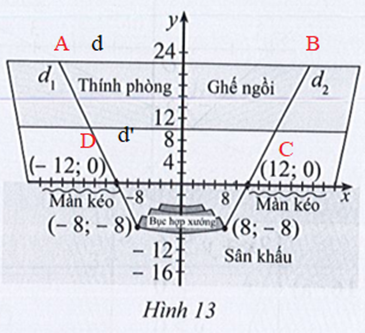
Phần chỗ ngồi của khán giả được giới hạn bởi các đường thẳng d1, d2, d và d’ chính là miền tứ giác ABCD.
Đường thẳng d đi qua điểm (0; 22) và song song với trục Ox nên có phương trình là y = 22.
Miền nghiệm nằm ở bên dưới nên ta có bất phương trình \(y \le 22\) (1)
Đường thẳng d’ đi qua điểm (0; 10) và song song với trục Ox nên có phương trình là y = 10.
Advertisements (Quảng cáo)
Miền nghiệm nằm ở bên trên đường thẳng d’ nên ta có bất phương trình y ≥ 10 (2) .
Gọi phương trình đường thẳng d1 là y = ax + b. \({d_1}\) đi qua hai điểm (– 12; 0) và (– 8; – 8) nên ta có:
\(\left\{ {\begin{array}{*{20}{c}}{ - 12a + b = 0}\\{ - 8a + b = - 8}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = - 2}\\{b = - 24}\end{array}} \right.\)
\( \Rightarrow {d_1}:y = - 2x - 24 \Leftrightarrow 2x + y = - 24\)
Điểm có tọa độ (0; 12) thuộc miền nghiệm ABCD và 2.0 + 12 = 12 > – 24 nên ta có bất phương trình 2x + y > – 24 (3).
Đường thẳng d2 có phương trình y = ax + b đi qua hai điểm (12; 0) và (8; – 8) nên ta có:
\(\left\{ {\begin{array}{*{20}{c}}{12a + b = 0}\\{8a + b = - 8}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = 2}\\{b = - 24}\end{array}} \right.\)
\( \Rightarrow {d_2}:y = 2x - 24 \Leftrightarrow 2x - y = 24\)
Điểm có tọa độ (0; 12) thuộc miền nghiệm ABCD và 2.0 – 12 = –12 < 24 nên ta có bất phương trình 2x – y < 24 (4).
Từ đó ta có hệ bất phương trình: \(\left\{ {\begin{array}{*{20}{c}}{2x + y > - 24}\\{2x - y < 24}\\{y \ge 10}\\{y \le 22}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{2x + y > - 24}\\{2x - y < 24}\\{10 \le y \le 22}\end{array}} \right.\)
