
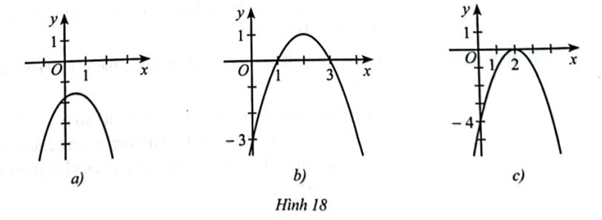
Dựa vào đồ thị hàm số bậc hai \(y = f\left( x \right)\) trong mỗi Hình 18a, 18b, 18c, hãy viết tập nghiệm các bất phương trình sau: \(f\left( x \right) > 0;f\left( x \right) < 0;f\left( x \right) \ge 0;f\left( x \right) \le 0\)

Phần đồ thị nằm dưới trục hoành tương ứng với \(f(x) < 0\)
Phần đồ thị nằm trên trục hoành tương ứng với \(f(x) > 0\)
Dựa vào parabol \(y = a{x^2} + bx + c\), ta tìm tập hợp những giá trị của \(x\) ứng với phần trên hoặc dưới trục hoành tùy dấu của tam thức bậc hai

a) Quan sát đồ thị ở Hình 18a, ta có đồ thị hàm số \(y = f(x)\) nằm phía dưới trục hoành và không cắt trục hoành nên \(f\left( x \right) < 0\) với mọi \(x \in \mathbb{R}\). Do đó:
+ Tập nghiệm của BPT \(f\left( x \right) > 0\) là \(S = \emptyset \)
+ Tập nghiệm của BPT \(f\left( x \right) < 0\) là \(S = \mathbb{R}\)
+ Tập nghiệm của BPT \(f\left( x \right) \ge 0\) là \(S = \emptyset \)
Advertisements (Quảng cáo)
+ Tập nghiệm của BPT \(f\left( x \right) \le 0\) là \(S = \mathbb{R}\)
b) Quan sát đồ thị ở Hình 18b, ta có:
Phần đồ thị nằm trên trục hoành ứng với \(1 < x < 3\)
Phần đồ thị nằm dưới trục hoành ứng với \(x < 1\) và \(x > 3\)
Đồ thị cắt trục hoành tại điểm có hoành độ \(x = 1\) và \(x = 3\)
Kết luận
+ Tập nghiệm của BPT \(f\left( x \right) > 0\) là \(S = \left( {1;3} \right)\)
+ Tập nghiệm của BPT \(f\left( x \right) < 0\) là \(S = \left( { - \infty ;1} \right) \cup \left( {3; + \infty } \right)\)
+ Tập nghiệm của BPT \(f\left( x \right) \ge 0\) là \(S = \left[ {1;3} \right]\)
+ Tập nghiệm của BPT \(f\left( x \right) \le 0\) là \(S = \left( { - \infty ;1} \right] \cup \left[ {3; + \infty } \right)\)
c) Quan sát đồ thị ở Hình 18c, ta có đồ thị hàm số \(y = f(x)\) nằm phía dưới trục hoành và cắt trục hoành tại A(2;0) nên \(f\left( x \right) \le 0\) với mọi \(x \in \mathbb{R}\).
+ Tập nghiệm của BPT \(f\left( x \right) > 0\) là \(S = \emptyset \)
+ Tập nghiệm của BPT \(f\left( x \right) < 0\) là \(S = \mathbb{R}{\rm{\backslash }}\{ 2\} \)
+ Tập nghiệm của BPT \(f\left( x \right) \ge 0\) là \(S = 2\)
+ Tập nghiệm của BPT \(f\left( x \right) \le 0\) là \(S = \mathbb{R}\)
