Cho tam giác ABC , biết cạnh \(a = 75\) cm, \(\widehat B = 80^\circ ,\widehat C = 40^\circ \)
a) Tính các góc, các cạnh còn lại của tam giác ABC
b) Tính bán kính đường tròn ngoại tiếp của tam giác ABC
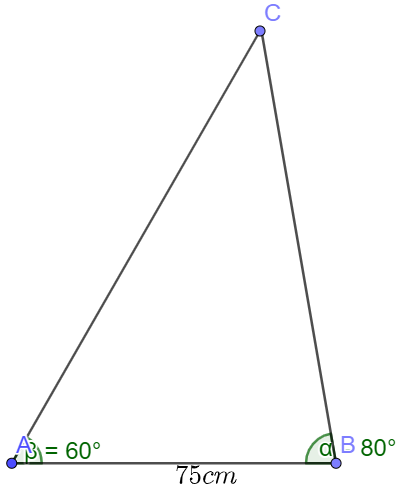
a) Ta có \(\widehat A + \widehat B + \widehat C = 180^\circ \)
Suy ra \(\widehat A = 180^\circ – \left( {\widehat B + \widehat C} \right) = 180^\circ – \left( {80^\circ + 40^\circ } \right) = 60^\circ \)
Áp dụng định lí sin ta có:
\(\begin{array}{l}\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = 2R\\ \Leftrightarrow \frac{{AB}}{{\sin 40^\circ }} = \frac{{75}}{{\sin 60^\circ }} = \frac{{AC}}{{\sin 80^\circ }} = 50\sqrt 3 \end{array}\)
\( \Rightarrow AB \simeq 55,67;AC \simeq 85,29\)
b) Ta có \(\frac{{BC}}{{\sin A}} = 2R \Rightarrow R = \frac{{BC}}{{2\sin A}} = \frac{{75}}{{2.\sin 60^\circ }} = 25\sqrt 3 \)