
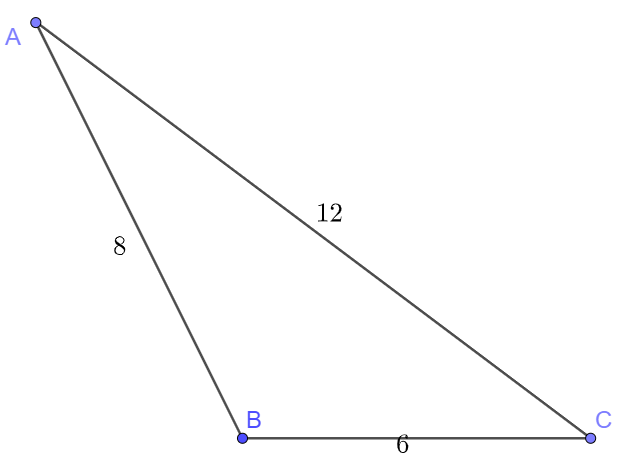
Tính góc lớn nhất của tam giác ABC, biết các cạnh là \(a = 8,b = 12,c = 6\)

Advertisements (Quảng cáo)
Áp dụng hệ quả của định lí côsin ta có:
\(\begin{array}{l}\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \frac{{{{12}^2} + {6^2} - {8^2}}}{{2.12.6}} = \frac{{29}}{{36}}\\ \Rightarrow \widehat A \simeq 36^\circ 20’\end{array}\)
\(\begin{array}{l}\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}} = \frac{{{8^2} + {6^2} - {{12}^2}}}{{2.8.6}} = - \frac{{11}}{{24}}\\ \Rightarrow \widehat B \simeq 117^\circ 17’\end{array}\)
\(\begin{array}{l}\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}} = \frac{{{8^2} + {{12}^2} - {6^2}}}{{2.12.8}} = \frac{{43}}{{48}}\\ \Rightarrow \widehat A \simeq 26^\circ 23’\end{array}\)
Ta thấy rằng \(117^\circ 17′ > 36^\circ 20′ > 26^\circ 23’\) nên góc B là góc lớn nhất trong tam giác ABC đã cho
