Advertisements (Quảng cáo)
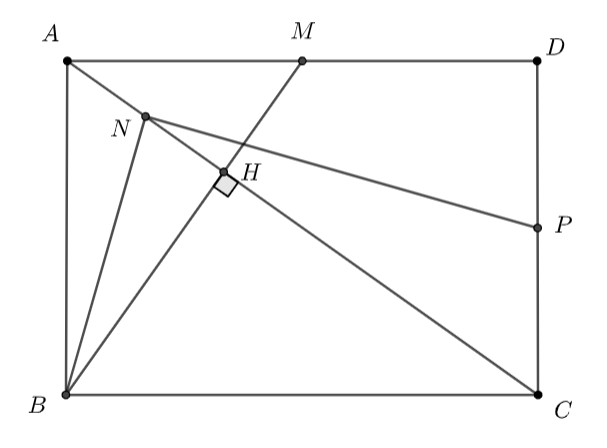
Cho hình chữ nhật \(ABCD\) có \(AB = 1,\,\,BC = \sqrt 2 .\) Gọi \(M\) là trung điểm của \(AD.\)
a) Chứng minh rằng các đường thẳng \(AC\) và \(BM\) vuông góc với nhau.
b) Gọi \(H\) là giao điểm của \(AC,\,\,BM.\) Gọi \(N\) là trung điểm của \(AH\) và \(P\) là trung điểm của \(CD.\) Chứng minh rằng tam giác \(NBP\) là một tam giác vuông.
– Tính các vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {BM} \) xong tính tích vô hướng của hai vectơ \(\overrightarrow {AC} .\overrightarrow {BM} \)
– Tính độ dài các cạnh \(AC,\,\,AH\)
– Tính các vectơ \(\overrightarrow {NB} \) và \(\overrightarrow {NP} \) xong tính tích vô hướng của hai vectơ \(\overrightarrow {NB} .\overrightarrow {NP} \)
a) Ta có: \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \) (quy tắc hình bình hành)
Ta có: \(\overrightarrow {BM} = \overrightarrow {AM} – \overrightarrow {AB} = \frac{1}{2}\overrightarrow {AD} – \overrightarrow {AB} \)
\( \Rightarrow \) \(\overrightarrow {AC} .\overrightarrow {BM} = \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right)\left( {\frac{1}{2}\overrightarrow {AD} – \overrightarrow {AB} } \right)\)
\(\begin{array}{l} = \frac{1}{2}\overrightarrow {AB} .\overrightarrow {AD} – {\overrightarrow {AB} ^2} + \frac{1}{2}{\overrightarrow {AD} ^2} – \overrightarrow {AB} .\overrightarrow {AD} \\ = – {\overrightarrow {AB} ^2} + \frac{1}{2}{\overrightarrow {AD} ^2} = – 1 + \frac{1}{2}\left( {\sqrt 2 } \right) – 1 + 1 = 0\end{array}\)
Advertisements (Quảng cáo)
\( \Rightarrow \) \(\overrightarrow {AC} \bot \overrightarrow {BM} \) \( \Rightarrow \) \(AC \bot BM\)
b) Xét \(\Delta ABC\) vuông tại \(B\) có:
\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {1 + {{\left( {\sqrt 2 } \right)}^2}} = \sqrt 3 \) (1)
Xét \(\Delta ABN\) vuông tại \(A\) có:
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{M^2}}}\) (hệ thức lượng trong tam giác vuông)
\( \Rightarrow \,\,\frac{1}{{A{H^2}}} = \frac{1}{{{1^2}}} + \frac{1}{{{{\left( {\frac{{\sqrt 2 }}{2}} \right)}^2}}} = 1 + 2 = 3\)
\( \Rightarrow \,\,AH = \frac{{\sqrt 3 }}{3}\) (2)
Từ (1) và (2) \( \Rightarrow \) \(AH = \frac{1}{3}AC\)
Ta có: \(\overrightarrow {NB} = \overrightarrow {AB} – \overrightarrow {AN} = \overrightarrow {AB} – \frac{1}{2}\overrightarrow {AH} = \overrightarrow {AB} – \frac{1}{6}\overrightarrow {AC} = \frac{5}{6}\overrightarrow {AB} – \frac{1}{6}\overrightarrow {AD} \)
Ta có: \(\overrightarrow {NP} = \overrightarrow {CP} – \overrightarrow {CN} = \frac{1}{2}\overrightarrow {CD} – \frac{5}{6}\overrightarrow {CA} = \frac{5}{6}\overrightarrow {AC} – \frac{1}{2}\overrightarrow {AB} = \frac{5}{6}\overrightarrow {AD} + \frac{1}{3}\overrightarrow {AB} \)
\( \Rightarrow \) \(\overrightarrow {NB} .\overrightarrow {NP} = \left( {\frac{5}{6}\overrightarrow {AB} – \frac{1}{6}\overrightarrow {AD} } \right)\left( {\frac{5}{6}\overrightarrow {AD} + \frac{1}{3}\overrightarrow {AB} } \right)\)
\(\begin{array}{l} = \frac{{25}}{{36}}\overrightarrow {AB} .\overrightarrow {AD} + \frac{5}{{18}}{\overrightarrow {AB} ^2} – \frac{5}{{36}}{\overrightarrow {AD} ^2} – \frac{1}{{18}}\overrightarrow {AB} .\overrightarrow {AD} \\ = \frac{5}{{18}}{\overrightarrow {AB} ^2} – \frac{5}{{36}}{\overrightarrow {AD} ^2} = \frac{5}{{18}}.1 – \frac{5}{{36}}.\left( {\sqrt 2 } \right) = \frac{5}{{18}} – \frac{5}{{18}} = 0\end{array}\)
\( \Rightarrow \) \(\overrightarrow {NB} \bot \overrightarrow {NP} \) \( \Rightarrow \) \(NB \bot NP\)
\( \Rightarrow \) \(\Delta NBP\) vuông tại \(N\).